题目内容
17. 质量为m的飞机以水平速度v0飞离跑道后逐渐上升,若飞机在此过程中水平速度保持不变,同时受到重力和竖直向上的恒定升力(该升力由其它力的合力提供,不含重力).今测得当飞机在水平方向的位移为l时,它的上升高度为h,则下列说法中正确的是( )
质量为m的飞机以水平速度v0飞离跑道后逐渐上升,若飞机在此过程中水平速度保持不变,同时受到重力和竖直向上的恒定升力(该升力由其它力的合力提供,不含重力).今测得当飞机在水平方向的位移为l时,它的上升高度为h,则下列说法中正确的是( )| A. | 从起飞到上升至h高度的时间为t=$\frac{1}{{v}_{0}}$ | |
| B. | 从起飞到上升至h高度的过程中飞机受到的升力大小为F升=$\frac{2mh{{v}_{0}}^{2}}{{l}^{2}}$ | |
| C. | 从起飞到上升至h高度的过程中升力所作的功为W升=$\frac{2m{h}^{2}{{v}_{0}}^{2}}{{l}^{2}}$+mgh | |
| D. | 在高度h处飞机的动能为Ek=$\frac{{l}^{2}+4{h}^{2}}{2{l}^{2}}$mv02 |
分析 飞机做类平抛运动,水平方向做匀速直线运动,由水平位移和速度求时间.根据运动学公式与牛顿第二定律相结合,可求解升力;根据功的表达式与动能表达式,即可求解升力所作的功及在高度h处飞机的动能.
解答 解:A、飞机水平速度不变,则有 l=v0t,得:t=$\frac{l}{{v}_{0}}$,故A正确.
B、y方向加速度恒定,h=$\frac{1}{2}$at2,即得:a=$\frac{2h{v}_{0}^{2}}{{l}^{2}}$
由牛顿第二定律得:F-mg=ma
得升力:F=mg(1+$\frac{2h{v}_{0}^{2}}{g{l}^{2}}$),故B错误.
C、升力做功为:W升=Fh=mgh(1+$\frac{2h{v}_{0}^{2}}{g{l}^{2}}$)=$\frac{2m{h}^{2}{{v}_{0}}^{2}}{{l}^{2}}$+mgh,故C正确.
D、在h处vt=at=$\sqrt{2ah}$,动能为:Ek=$\frac{1}{2}$m(v02+vt2),联立解得:Ek=$\frac{1}{2}$mv02(1+$\frac{4{h}^{2}}{{l}^{2}}$)=$\frac{{l}^{2}+4{h}^{2}}{2{l}^{2}}$mv02.故D正确.
故选:ACD.
点评 此题考查物体做类平抛运动中,运动学公式与牛顿第二定律相综合运用,并掌握功与动能表达式,同时学会运动的分解与合成的应用.

练习册系列答案
相关题目
8.关于位移和路程,下列说法不正确的是( )
| A. | 位移是矢量,路程是标量 | |
| B. | 路程不等,但位移可能相同 | |
| C. | 路程不为零,但位移可能是零 | |
| D. | 质点做直线运动时,通过的路程是位移 |
5.小船匀速逆流而上,经过桥下时箱子落水了,船继续前进一段时间后才发现,并立即调头以相同的静水船速顺流而下,经过1h在下游距桥7.2km处追上.若认为认为箱子落水即与河水有共同速度,则河水流动速度为( )
| A. | 7.2km/h | B. | 3.6km/h | ||
| C. | 1m/s | D. | 条件不足,无法确定 |
12.为了探究做功与物体速度变化间的关系,现提供如图(1)所示的装置,让小车在橡皮筋的作用下弹出后,沿木板滑行,请思考探究思路并回答下列问题(打点计时器所接交流电频率为50Hz).
(1)为了消除摩擦力的影响应采取什么措施:将木板固定有打点计时器的一端垫起适当的高度,使小车缓慢匀速下滑..
(2)当我们分别用同样的橡皮筋1条、2条、3条…并起来分别进行第1次、第2次、第3次…实验时,每次实验中橡皮筋拉伸的长度都应该保持一致,我们把第1次实验时橡皮筋对小车做的功记为W;
(3)由于橡皮筋对小车做功而使小车获得的速度可以由打点计时器打出的纸带测出,如图(2)所示是其中四次实验打出的部分纸带;

(4)试根据第(2)、(3)步骤中的信息,填写表;
(5)试在图(3)、(4)中作出相应的函数图象:

(6)实验结论是:橡皮筋对小车做功与小车速度的平方成正比.
(1)为了消除摩擦力的影响应采取什么措施:将木板固定有打点计时器的一端垫起适当的高度,使小车缓慢匀速下滑..
(2)当我们分别用同样的橡皮筋1条、2条、3条…并起来分别进行第1次、第2次、第3次…实验时,每次实验中橡皮筋拉伸的长度都应该保持一致,我们把第1次实验时橡皮筋对小车做的功记为W;
(3)由于橡皮筋对小车做功而使小车获得的速度可以由打点计时器打出的纸带测出,如图(2)所示是其中四次实验打出的部分纸带;

(4)试根据第(2)、(3)步骤中的信息,填写表;
| 次数 | 1 | 2 | 3 | 4 |
| 橡皮筋对小车做功 | W | |||
| 小车速度v(m/s) | ||||
| v2(m2/s2) |

(6)实验结论是:橡皮筋对小车做功与小车速度的平方成正比.
2. 如图所示,A、B两球质量相等,开始两球静止,将A上方的细绳烧断,在B落地之前,以两球和弹簧为一研究系统,在任一时刻,下列说法正确的是(不计空气阻力)( )
如图所示,A、B两球质量相等,开始两球静止,将A上方的细绳烧断,在B落地之前,以两球和弹簧为一研究系统,在任一时刻,下列说法正确的是(不计空气阻力)( )
 如图所示,A、B两球质量相等,开始两球静止,将A上方的细绳烧断,在B落地之前,以两球和弹簧为一研究系统,在任一时刻,下列说法正确的是(不计空气阻力)( )
如图所示,A、B两球质量相等,开始两球静止,将A上方的细绳烧断,在B落地之前,以两球和弹簧为一研究系统,在任一时刻,下列说法正确的是(不计空气阻力)( )| A. | 两球的加速度相同 | B. | 两球的动能相等 | ||
| C. | 系统的机械能守恒 | D. | 弹簧对A、B两球做功之和为零 |
9. 如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,则物体A的运动情况是:( )
如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,则物体A的运动情况是:( )
 如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,则物体A的运动情况是:( )
如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,则物体A的运动情况是:( )| A. | 匀速上升 | B. | 加速上升 | C. | 先加速后减速 | D. | 减速上升 |
6.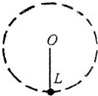 如图所示,长为L的轻杆,一端固定一个小球,另一端固定在光滑的水平轴上,使小球在竖直平面内作圆周运动,关于小球在最高点的速度v下列说法中正确的是( )
如图所示,长为L的轻杆,一端固定一个小球,另一端固定在光滑的水平轴上,使小球在竖直平面内作圆周运动,关于小球在最高点的速度v下列说法中正确的是( )
 如图所示,长为L的轻杆,一端固定一个小球,另一端固定在光滑的水平轴上,使小球在竖直平面内作圆周运动,关于小球在最高点的速度v下列说法中正确的是( )
如图所示,长为L的轻杆,一端固定一个小球,另一端固定在光滑的水平轴上,使小球在竖直平面内作圆周运动,关于小球在最高点的速度v下列说法中正确的是( )| A. | v的最小值为$\sqrt{gL}$ | |
| B. | v由零逐渐增大,向心力也逐渐增大 | |
| C. | 当v由$\sqrt{gL}$值逐渐增大时,杆对小球的弹力逐渐增大 | |
| D. | 当v由$\sqrt{gL}$值逐渐减小时,杆对小球的弹力逐渐减小 |
7. 如图所示,有四块相同的坚固石块垒成弧形的石拱,每块石块的质量均为m,每块石块的两个面间所夹的圆心角均为30°,第3、第4块固定在地面上,假定石块间的摩擦力可以忽略不计,则第1与第2石块的作用力大小为( )
如图所示,有四块相同的坚固石块垒成弧形的石拱,每块石块的质量均为m,每块石块的两个面间所夹的圆心角均为30°,第3、第4块固定在地面上,假定石块间的摩擦力可以忽略不计,则第1与第2石块的作用力大小为( )
 如图所示,有四块相同的坚固石块垒成弧形的石拱,每块石块的质量均为m,每块石块的两个面间所夹的圆心角均为30°,第3、第4块固定在地面上,假定石块间的摩擦力可以忽略不计,则第1与第2石块的作用力大小为( )
如图所示,有四块相同的坚固石块垒成弧形的石拱,每块石块的质量均为m,每块石块的两个面间所夹的圆心角均为30°,第3、第4块固定在地面上,假定石块间的摩擦力可以忽略不计,则第1与第2石块的作用力大小为( )| A. | mg | B. | $\frac{2\sqrt{3}}{3}$mg | C. | 2mg | D. | $\sqrt{3}$mg |
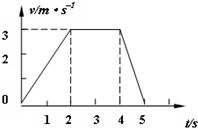 如图是一质点的速度时间图象,由图象可知:
如图是一质点的速度时间图象,由图象可知: