题目内容
2.已知质量为m的木块的大小为F的水平拉力作用下沿粗糙水平地面做匀加速直线运动,加速度为a,则木块与地面之间的动摩擦因数为$\frac{T-ma}{mg}$.若在木块上再施加一个与水平拉力F在同一竖直平面内的推力,而不改变木块的加速度的大小和方向,则此推力与水平拉力F的夹角为$arctan\frac{mg}{T-ma}$.分析 对物体进行受力分析,物体在水平方向受拉力、摩擦力,竖直方向受重力和地面支持力,根据牛顿第二定律分析.当加推力时物体受五个力:重力、支持力、拉力、摩擦和和推力,根据受力分析求解即可.
解答 解:(1)如图对物体进行受力分析有: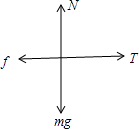
T-f=ma ①
f=μN=μmg ②
由①和②得:$μ=\frac{T-ma}{mg}$
(2)如图,当有推力作用时,令推力与T成θ角,则此时物体产生的加速度为a
由有:
水平方向:T+Fcosθ-f=ma ③
竖直方向:N-mg-Fsinθ=0 ④
摩擦力大小为:f=μN ⑤
由④⑤⑥和$μ=\frac{T-ma}{mg}$可得:
tanθ=$\frac{1}{μ}$=$\frac{mg}{T-ma}$
解得:θ=$arctan\frac{mg}{T-ma}$
故答案为:$\frac{T-ma}{mg}$,$arctan\frac{mg}{T-ma}$
点评 正确的受力分析求出合外力,根据牛顿第二定律确定合外力与加速度的关系是解决本题的关键.

练习册系列答案
相关题目
12.下列说法中正确的是( )
| A. | 一个力只能分解成唯一确定的一对分力 | |
| B. | .同一个力,不加任何限制条件,可以分解成无数对分力 | |
| C. | 已知合力和它的两个分力的方向,则两个分力有确定值 | |
| D. | 已知合力和它的一个分力的大小,另一分力的方向,则分解是唯一的 |
13.作变速直线运动的物体,若前一半位移的平均速度为2m/s,后一半位移的平均速度是8m/s,则全程的平均速度是( )
| A. | 7 m/s | B. | 5 m/s | C. | 6 m/s | D. | 3.2 m/s |
10. 如图所示,高为h=1.25m的平台上,覆盖一层薄冰,现有一质量为60kg的滑雪爱好者,以一定的初速度v向平台边缘滑去,着地时的速度方向与水平地面的夹角为45°(取重力加速度g=10m/s2).由此可知下列各项中错误的是( )
如图所示,高为h=1.25m的平台上,覆盖一层薄冰,现有一质量为60kg的滑雪爱好者,以一定的初速度v向平台边缘滑去,着地时的速度方向与水平地面的夹角为45°(取重力加速度g=10m/s2).由此可知下列各项中错误的是( )
 如图所示,高为h=1.25m的平台上,覆盖一层薄冰,现有一质量为60kg的滑雪爱好者,以一定的初速度v向平台边缘滑去,着地时的速度方向与水平地面的夹角为45°(取重力加速度g=10m/s2).由此可知下列各项中错误的是( )
如图所示,高为h=1.25m的平台上,覆盖一层薄冰,现有一质量为60kg的滑雪爱好者,以一定的初速度v向平台边缘滑去,着地时的速度方向与水平地面的夹角为45°(取重力加速度g=10m/s2).由此可知下列各项中错误的是( )| A. | 滑雪者离开平台边缘时的速度大小是5.0m/s | |
| B. | 滑雪者着地点到平台边缘的水平距离是2.5m | |
| C. | 滑雪者在空中运动的时间为1s | |
| D. | 着地时滑雪者重力做功的瞬时功率是300W |
17. 如图所示的电路中,L1和L2是两个相同的小灯泡,L是一个自感系数较大、直流电阻可忽略不计的理想线圈,在电键S接通和断开时,下列观察到的现象正确的是( )
如图所示的电路中,L1和L2是两个相同的小灯泡,L是一个自感系数较大、直流电阻可忽略不计的理想线圈,在电键S接通和断开时,下列观察到的现象正确的是( )
 如图所示的电路中,L1和L2是两个相同的小灯泡,L是一个自感系数较大、直流电阻可忽略不计的理想线圈,在电键S接通和断开时,下列观察到的现象正确的是( )
如图所示的电路中,L1和L2是两个相同的小灯泡,L是一个自感系数较大、直流电阻可忽略不计的理想线圈,在电键S接通和断开时,下列观察到的现象正确的是( )| A. | 当电键S接通时,灯泡L1缓慢亮起来,L2立即亮起来 | |
| B. | 当电键S接通时,灯炮L1和L2都缓慢亮起来 | |
| C. | 当电键S断开时,灯炮L2闪亮一下,然后才逐渐熄灭 | |
| D. | 当电键S断开时,灯泡L2不会闪亮,只是逐渐熄灭 |
14.一质量为m,电量为q的微观粒子沿垂直场强方向从中央射入两平行带电板之间,当粒子的入射速度为v0时,恰好能穿越平行板电场,为使其入射速度减半时仍恰能穿越电场,则必须使得( )
| A. | 粒子的电量减半 | B. | 两板间电压减半 | C. | 两板间距加倍 | D. | 两板间距减半 |
5.一质量m=1kg的小球,由距离水平地面H=4m处静止释放,已知小球下落加速度a=8m/s2,下落过程中阻力恒定,g=10m/s2,则下列说法正确的是( )
| A. | 小球下落过程中机械能守恒 | |
| B. | 小球落地时重力的瞬时功率为80W | |
| C. | 小球从释放到落地重力势能减少了32J | |
| D. | 小球从释放到落地动能增加了40J |
 如图所示,质量为m1=2kg的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.设最大静摩擦力等于滑动摩擦力,求:
如图所示,质量为m1=2kg的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.设最大静摩擦力等于滑动摩擦力,求: