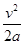题目内容
平直的公路上,甲车匀速行驶,速度为10m/s,当它经过乙车处时,乙车从静止开始以a=1m/s2的加速度作匀加速运动,方向与甲车运动方向相同.
求(1)乙车追上甲车前,它们的最大距离?
(2)乙车经过多长时间追上甲车?
求(1)乙车追上甲车前,它们的最大距离?
(2)乙车经过多长时间追上甲车?
分析:(1)抓住两车相距最大时的临界条件:两车速度相等展开计算即可;
(2)乙车追上甲车时两车相对乙车起点的位移相等,根据位移时间关系求解即可.
(2)乙车追上甲车时两车相对乙车起点的位移相等,根据位移时间关系求解即可.
解答:解:(1)乙车追上甲车前,它们距离最大时两车速度相等,即此时v乙=v甲=10m/s
因为乙车做速度为0的,加速度为1m/s2的匀加速直线运动,据速度时间关系v乙=at,两车位移最大时两车运动的时间t=
s=10s
两车的最大距离△xmax=v甲t-
at2=10×10-
×1×102m=50m;
(2)当乙车追上甲车时,相对于乙车出发点的位移满足:
x乙=x甲
即:
at2=v甲t
代入数据可得t=20s.
答:(1)乙车追上甲车前,它们的最大距离为50m;
(2)乙车经过多长20s追上甲车.
因为乙车做速度为0的,加速度为1m/s2的匀加速直线运动,据速度时间关系v乙=at,两车位移最大时两车运动的时间t=
| 10 |
| 1 |
两车的最大距离△xmax=v甲t-
| 1 |
| 2 |
| 1 |
| 2 |
(2)当乙车追上甲车时,相对于乙车出发点的位移满足:
x乙=x甲
即:
| 1 |
| 2 |
代入数据可得t=20s.
答:(1)乙车追上甲车前,它们的最大距离为50m;
(2)乙车经过多长20s追上甲车.
点评:掌握两车相距最远时的临界条件和追击条件是解决本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目