题目内容
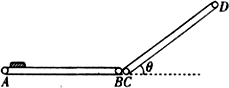
图示为仓库中常用的皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B 两端相距3m ,另一台倾斜,传送带与地面的倾角θ= 37°, C、D 两端相距4.45m , B、C相距很近.水平部分AB 以5m/s的速率顺时针转动.将质量为10 kg 的一袋大米放在A 端,到达B 端后,速度大小不变地传到倾斜的CD 部分,米袋与传送带间的动摩擦因数均为0.5.(g=10m/s2 ,sin37°=0.6,cos37°=0.8,可能用到数据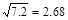 )
)
(1)若CD 部分传送带不运转,求米袋沿传送带所能上升的最大距离.
(2)若要使米袋能被送到D 端,求CD 部分顺时针运转的速度应满足的条件及米袋从C 端到D 端所用时间的取值范围.
(1)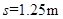
(2)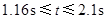
【解析】(1)米袋在AB上加速时的加速度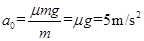 (1分)
(1分)
米袋的速度达到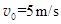 时,滑行的距离
时,滑行的距离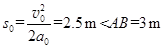 ,因此米袋在到达B点之前就有了与传送带相同的速度
(1分)
,因此米袋在到达B点之前就有了与传送带相同的速度
(1分)
设米袋在CD上运动的加速度大小为a,由牛顿第二定律得
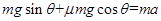 (1分)
(1分)
代入数据得
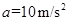 (1分)
(1分)
所以能滑上的最大距离 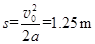 (2分)
(2分)
(2)设CD部分运转速度为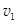 时米袋恰能到达D点(即米袋到达D点时速度恰好为零),则米袋速度减为
时米袋恰能到达D点(即米袋到达D点时速度恰好为零),则米袋速度减为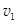 之前的加速度为
之前的加速度为
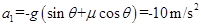 (2分)
(2分)
米袋速度小于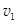 至减为零前的加速度为
至减为零前的加速度为
 (2分)
(2分)
由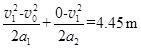 (1分)
(1分)
解得 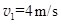 ,即要把米袋送到D点,CD部分的速度
,即要把米袋送到D点,CD部分的速度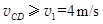 (1分)
(1分)
米袋恰能运到D点所用时间最长为
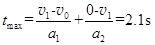 (1分)
(1分)
若CD部分传送带的速度较大,使米袋沿CD上滑时所受摩擦力一直沿皮带向上,
则所用时间最短,此种情况米袋加速度一直为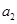 。
。
由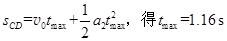 (2分)
(2分)
所以,所求的时间t的范围为 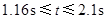 (1分)
(1分)

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案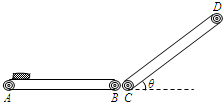 (2011?湖北模拟)图示为仓库中常用的皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B 两端相距3m,另一台倾斜,传送带与地面的倾角θ=37°,C、D 两端相距4.45m,B、C相距很近.水平部分AB 以5m/s的速率顺时针转动.将质量为10kg 的一袋大米放在A 端,到达B 端后,速度大小不变地传到倾斜的CD 部分,米袋与传送带间的动摩擦因数均为0.5.(g取10m/s2)试求:
(2011?湖北模拟)图示为仓库中常用的皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B 两端相距3m,另一台倾斜,传送带与地面的倾角θ=37°,C、D 两端相距4.45m,B、C相距很近.水平部分AB 以5m/s的速率顺时针转动.将质量为10kg 的一袋大米放在A 端,到达B 端后,速度大小不变地传到倾斜的CD 部分,米袋与传送带间的动摩擦因数均为0.5.(g取10m/s2)试求: 图示为仓库中常用的皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B 两端相距3m,另一台倾斜,传送带与地面的倾角θ=37°,C、D 两端相距4.45m,B、C相距很近.水平部分AB 以5m/s的速率顺时针转动.将质量为10kg 的一袋大米轻轻放在A 端,到达B 端后,速度大小不变地传到倾斜的CD 部分,米袋与传送带间的动摩擦因数均为0.5.
图示为仓库中常用的皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B 两端相距3m,另一台倾斜,传送带与地面的倾角θ=37°,C、D 两端相距4.45m,B、C相距很近.水平部分AB 以5m/s的速率顺时针转动.将质量为10kg 的一袋大米轻轻放在A 端,到达B 端后,速度大小不变地传到倾斜的CD 部分,米袋与传送带间的动摩擦因数均为0.5. (2012?桂林模拟)如图示为仓库中常用的皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B 两端相距L1=3m,另一台倾斜,传送带与地面的倾角θ=37°,C、D 两端相距L2=2.8m,B、C相距很近.水平部分AB以υ1=5m/s的速率顺时针运转,倾斜部分CD以υ2=3m/s的速率顺时针运转.将质量为m=50kg 的一袋大米放在A 端,到达B 端后,速度大小不变地传到倾斜的CD 部分,米袋与传送带间的动摩擦因数均为0.5.求:米袋从A端到D 端所用的时间.
(2012?桂林模拟)如图示为仓库中常用的皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B 两端相距L1=3m,另一台倾斜,传送带与地面的倾角θ=37°,C、D 两端相距L2=2.8m,B、C相距很近.水平部分AB以υ1=5m/s的速率顺时针运转,倾斜部分CD以υ2=3m/s的速率顺时针运转.将质量为m=50kg 的一袋大米放在A 端,到达B 端后,速度大小不变地传到倾斜的CD 部分,米袋与传送带间的动摩擦因数均为0.5.求:米袋从A端到D 端所用的时间.