题目内容
如图所示的水平转盘可绕竖直轴OO′旋转,盘上水平杆上穿着两个质量均为 的小球A和B。现将A和B分别置于距轴
的小球A和B。现将A和B分别置于距轴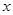 和
和 处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是
处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是 。试分析转速
。试分析转速 从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,
从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下, 与
与 、
、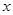 、
、 的关系式。
的关系式。

(1)绳中刚出现张力时;
(2)A球所受的摩擦力方向改变时;
(3)两球相对轴刚要滑动时。
【答案】
(1) (2)
(2) (3)
(3)
【解析】
试题分析:(1)B首先达到最大静摩擦力


(2)A受摩擦力恰好为0时:
对B: ①
①
对A: ② 联立解得:
② 联立解得:
(3)刚要滑动时:对B:
对A: 联立解得:
联立解得:
考点:牛顿第二定律;静摩擦力和最大静摩擦力;向心力.
点评:在转动过程中,两物体都需要向心力来维持,一开始是静摩擦力作为向心力,当摩擦力不足以做摩擦力时,
绳子的拉力就会来做补充,速度再快,当这2个力的合力都不足以做向心力时,物体将会发生相对滑动,

练习册系列答案
相关题目
 如图所示的水平转盘可绕竖直轴OO′旋转,盘上水平杆上穿着两个质量均为m的小球A和B.现将A和B分别置于距轴x和2x处,并用不可伸长的轻绳相连.已知两球与杆之间的最大静摩擦力都是fm.试分析转速ω从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,ω与m、x、fm的关系式.
如图所示的水平转盘可绕竖直轴OO′旋转,盘上水平杆上穿着两个质量均为m的小球A和B.现将A和B分别置于距轴x和2x处,并用不可伸长的轻绳相连.已知两球与杆之间的最大静摩擦力都是fm.试分析转速ω从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,ω与m、x、fm的关系式.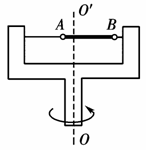
 的小球A和B。现将A和B分别置于距轴
的小球A和B。现将A和B分别置于距轴 和
和 处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是
处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是 。试分析转速
。试分析转速 从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,
从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,
 的小球A和B。现将A和B分别置于距轴
的小球A和B。现将A和B分别置于距轴 和
和 处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是
处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是 。试分析转速
。试分析转速 从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,
从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,