题目内容
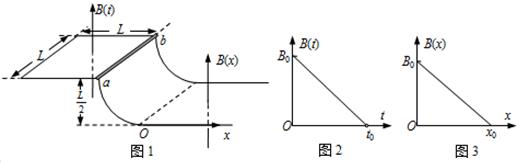
5.如图1所示,一端封闭的两条平行光滑长导轨相距L,距左端L处的右侧一段被弯成半径为$\frac{L}{2}$的四分之一圆弧,圆弧导轨的左、右两段处于高度相差$\frac{L}{2}$的水平面上.以弧形导轨的末端点O为坐标原点,水平向右为x轴正方向,建立Ox坐标轴.圆弧导轨所在区域无磁场;左段区域存在空间上均匀分布,但随时间t均匀变化的磁场B(t),如图2所示;右段区域存在磁感应强度大小不随时间变化,只沿x方向均匀变化的磁场B(x),如图3所示;磁场B(t)和B(x)的方向均竖直向上.在圆弧导轨最上端,放置一质量为m的金属棒ab,与导轨左段形成闭合回路,金属棒由静止开始下滑时左段磁场B(t)开始变化,金属棒与导轨始终接触良好,经过时间t0金属棒恰好滑到圆弧导轨底端.已知金属棒在回路中的电阻为R,导轨电阻不计,重力加速度为g.求:(1)金属棒在圆弧轨道上运动过程中,回路中产生的焦耳热;
(2)通过计算,确定金属棒在全部运动过程中感应电流最大时的位置.
分析 (1)由法拉第电磁感应定律求出感应电动势,然后求出产生的热量.
(2)分析清楚金属棒的运动过程,然后根据运动过程确定感应电流最大的位置.
解答 解:(1)金属棒下滑过程产生的感应电动势:E=$\frac{△Φ}{△t}$=$\frac{△B}{△t}$S=$\frac{{B}_{0}{L}^{2}}{{t}_{0}}$,
回路中产生的焦耳热:Q=$\frac{{E}^{2}}{R}$t0=$\frac{{B}_{0}^{2}{L}^{4}}{R{t}_{0}}$;
(2)金属棒沿圆弧轨道下滑时做加速运动,
金属棒进入水平轨道后做减速运动,
因此金属棒滑到圆弧轨道底端时速度v最大,
即:x=0时金属棒的速度最大,
由图3所示图象可知,x=0时B最大,
感应电流:I=$\frac{BLv}{R}$,B、v最大时,感应电流最大,
由于在x=0处,B、v最大,因此在x=0处感应电流最大;
答:(1)金属棒在圆弧轨道上运动过程中,回路中产生的焦耳热为$\frac{{B}_{0}^{2}{L}^{4}}{R{t}_{0}}$;
(2)金属棒在全部运动过程中感应电流最大时的位置是x=0处.
点评 本题考查了求焦耳热、判断感应电流最大的位置,分析清楚金属棒的运动过程是解题的关键,由于法拉第电磁感应定律与电功公式可以解题.

练习册系列答案
相关题目
16.下列说法正确的是( )
| A. | 力是维持物体运动的原因 | |
| B. | 作用力和反作用力可以是不同性质的力 | |
| C. | 静摩擦力的方向可以与速度方向共线或成一夹角 | |
| D. | 牛顿第一定律可以通过实验进行验证 |
13.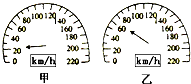 如图所示是一沿笔直公路做直线运动的汽车的速度计,某同学在汽车中观察速度计指针位置的变化,开始时指针指示在如图甲所示的位置,经过7s后指针如图乙,下列说法正确的是( )
如图所示是一沿笔直公路做直线运动的汽车的速度计,某同学在汽车中观察速度计指针位置的变化,开始时指针指示在如图甲所示的位置,经过7s后指针如图乙,下列说法正确的是( )
 如图所示是一沿笔直公路做直线运动的汽车的速度计,某同学在汽车中观察速度计指针位置的变化,开始时指针指示在如图甲所示的位置,经过7s后指针如图乙,下列说法正确的是( )
如图所示是一沿笔直公路做直线运动的汽车的速度计,某同学在汽车中观察速度计指针位置的变化,开始时指针指示在如图甲所示的位置,经过7s后指针如图乙,下列说法正确的是( )| A. | 速度计直接读出的是汽车运动的平均速度 | |
| B. | 速度计直接读出的是汽车运动的瞬时速度 | |
| C. | 汽车运动的加速度约为5.7 m/s2 | |
| D. | 汽车运动的加速度约为1.6 m/s2 |
10.关于电磁波,正确的说法是( )
| A. | 空间有变化的电场存在,一定能形成电磁波 | |
| B. | 在真空中电磁波的传播速度小于真空中的光速 | |
| C. | 电磁波只能在真空中传播,不能在介质中传播 | |
| D. | 电磁场具有能量 |
14.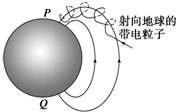 我国第21次南极科考队在南极观看到了美丽的极光.极光是由来自太阳的高能带电粒子流高速冲进高空稀薄大气层时,被地球磁场俘获,从而改变原有运动方向,向两极做螺旋运动(如图4所示),这些高能粒子在运动过程中与大气分子或原子剧烈碰撞或摩擦从而激发大气分子或原子,使其发出有一定特征的各种颜色的光.地磁场的存在,使多数宇宙粒子不能到达地面而向人烟稀少的两极偏移,为地球生命的诞生和维持提供了天然的屏障.科学家发现并证实,向两极做螺旋运动的这些高能粒子的旋转半径是不断减小的,这主要与下列哪些因素有关( )
我国第21次南极科考队在南极观看到了美丽的极光.极光是由来自太阳的高能带电粒子流高速冲进高空稀薄大气层时,被地球磁场俘获,从而改变原有运动方向,向两极做螺旋运动(如图4所示),这些高能粒子在运动过程中与大气分子或原子剧烈碰撞或摩擦从而激发大气分子或原子,使其发出有一定特征的各种颜色的光.地磁场的存在,使多数宇宙粒子不能到达地面而向人烟稀少的两极偏移,为地球生命的诞生和维持提供了天然的屏障.科学家发现并证实,向两极做螺旋运动的这些高能粒子的旋转半径是不断减小的,这主要与下列哪些因素有关( )
 我国第21次南极科考队在南极观看到了美丽的极光.极光是由来自太阳的高能带电粒子流高速冲进高空稀薄大气层时,被地球磁场俘获,从而改变原有运动方向,向两极做螺旋运动(如图4所示),这些高能粒子在运动过程中与大气分子或原子剧烈碰撞或摩擦从而激发大气分子或原子,使其发出有一定特征的各种颜色的光.地磁场的存在,使多数宇宙粒子不能到达地面而向人烟稀少的两极偏移,为地球生命的诞生和维持提供了天然的屏障.科学家发现并证实,向两极做螺旋运动的这些高能粒子的旋转半径是不断减小的,这主要与下列哪些因素有关( )
我国第21次南极科考队在南极观看到了美丽的极光.极光是由来自太阳的高能带电粒子流高速冲进高空稀薄大气层时,被地球磁场俘获,从而改变原有运动方向,向两极做螺旋运动(如图4所示),这些高能粒子在运动过程中与大气分子或原子剧烈碰撞或摩擦从而激发大气分子或原子,使其发出有一定特征的各种颜色的光.地磁场的存在,使多数宇宙粒子不能到达地面而向人烟稀少的两极偏移,为地球生命的诞生和维持提供了天然的屏障.科学家发现并证实,向两极做螺旋运动的这些高能粒子的旋转半径是不断减小的,这主要与下列哪些因素有关( )| A. | 洛伦兹力对粒子做负功,使其动能减小 | |
| B. | 空气阻力做负功,使其动能减小 | |
| C. | 靠近南北两极,磁感应强度增强 | |
| D. | 以上说法都不对 |
15.物体由静止开始运动,加速度恒定,在第7s内的初速度是2.6m/s,则物体的加速度是( )
| A. | 0.33m/s2 | B. | 0.37m/s2 | C. | 2.6m/s2 | D. | 0.43m/s2 |
 一空间存在匀强电场,场中A、B、C、D四个点恰好构成正四面体,如图所示.已知电场强度大小为E,方向平行于正四面体的底面ABC,正四面体棱长为2$\sqrt{3}$cm.已知UAC=6V、UBC=6V,求:
一空间存在匀强电场,场中A、B、C、D四个点恰好构成正四面体,如图所示.已知电场强度大小为E,方向平行于正四面体的底面ABC,正四面体棱长为2$\sqrt{3}$cm.已知UAC=6V、UBC=6V,求: