题目内容
 如图所示,用细线悬挂一个小球,在水平恒力F作用下小球能在B处静止,现用该恒力F将小球由静止从竖直位置A拉到位置B,此时线与竖直方向的夹角为θ,则有( )
如图所示,用细线悬挂一个小球,在水平恒力F作用下小球能在B处静止,现用该恒力F将小球由静止从竖直位置A拉到位置B,此时线与竖直方向的夹角为θ,则有( )分析:因小球力为恒力,故可直接利用功的公式W=FLcosθ求解,而重力做功根据WG=mgh,再由B点处于平衡可得F与G的关系.从而根据动能定理即可求解.
解答:解:A、由A到B的过程中恒力F做的功大于小球势能的增量,故A错误;
B、由几何关系可知,从A到B的高度为h=L-Lcosθ
所以重力的功为:WG=-mg(L-Lcosθ),
通过计算得:WF>WG,则由动能定理,有小球在B点的速度不为零,故B错误;
C、对B点受力分析,重力G,拉力F,细线的拉力T,由于处于平衡,由力的分解可得,F=mgtanθ;
从A到B过程中,拉力做功为,WF=FLsinθ;细线的拉力始终与速度方向垂直,所以不做功.故C正确;
D、若在B点将力F撤去,由于存在速度,所以小球来回摆动时偏离竖直方向的最大角度大于θ,故D正确;
故选:CD
B、由几何关系可知,从A到B的高度为h=L-Lcosθ
所以重力的功为:WG=-mg(L-Lcosθ),
通过计算得:WF>WG,则由动能定理,有小球在B点的速度不为零,故B错误;
C、对B点受力分析,重力G,拉力F,细线的拉力T,由于处于平衡,由力的分解可得,F=mgtanθ;
从A到B过程中,拉力做功为,WF=FLsinθ;细线的拉力始终与速度方向垂直,所以不做功.故C正确;
D、若在B点将力F撤去,由于存在速度,所以小球来回摆动时偏离竖直方向的最大角度大于θ,故D正确;
故选:CD
点评:本题要求学生能正确理解功的定义式的含义及适用条件为恒力做功,同时注意先找出物体的位移及拉力

练习册系列答案
相关题目
 如图所示,用细线悬挂的铝圆环和磁铁在同一竖直平面内,当圆环通入方向如图所示的电流时,圆环将( )
如图所示,用细线悬挂的铝圆环和磁铁在同一竖直平面内,当圆环通入方向如图所示的电流时,圆环将( ) 如图所示,用细线悬挂的带正电的小球质量为m,处在水平向右的匀强电场中.在电场力作用下,小球由最低点开始运动,经过b点后还可以向右摆动,则在小球由a摆到b这一过程中,下列说法正确的是( )
如图所示,用细线悬挂的带正电的小球质量为m,处在水平向右的匀强电场中.在电场力作用下,小球由最低点开始运动,经过b点后还可以向右摆动,则在小球由a摆到b这一过程中,下列说法正确的是( ) 如图所示,用细线悬挂的小球从A点开始摆动,经过最低点B时摆线被直尺P挡住,球继续摆动至C点.若不计空气阻力,下列说法正确的是( )
如图所示,用细线悬挂的小球从A点开始摆动,经过最低点B时摆线被直尺P挡住,球继续摆动至C点.若不计空气阻力,下列说法正确的是( )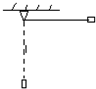 如图所示,用细线悬挂一小铁块,将小铁块拉直到如图所示的水平位置,然后放手使小块从静止开始向下摆动,在小铁块摆向最低点的过程中,重力对小铁块做功的功率( )
如图所示,用细线悬挂一小铁块,将小铁块拉直到如图所示的水平位置,然后放手使小块从静止开始向下摆动,在小铁块摆向最低点的过程中,重力对小铁块做功的功率( )