题目内容
17.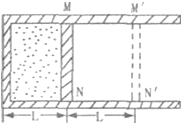 如图所示是一个右端开口的圆筒形气缸,活塞可以在气缸内自由滑动.活塞将一定量的理想气体封闭在气缸内,此时气体的温度为27℃.若给气缸加热,使气体温度升高,让气体推动活塞从MN缓慢地移到M′N′.已知大气压强P0=1×105Pa.求:
如图所示是一个右端开口的圆筒形气缸,活塞可以在气缸内自由滑动.活塞将一定量的理想气体封闭在气缸内,此时气体的温度为27℃.若给气缸加热,使气体温度升高,让气体推动活塞从MN缓慢地移到M′N′.已知大气压强P0=1×105Pa.求:(1)当活塞到达M′N′后气体的温度.
(2)把活塞锁定在M′N′位置上,让气体的温度缓慢地变回到27℃,此时
气体的压强是多少?画出在此过程中气体压强P随温度T变化的图象.
分析 (1)由盖吕萨克定律可以求出气体的温度;
(2)由查理定律可以求出气体的压强,然后作出图象.
解答 解:(1)在活塞移动过程中,气体压强不变,是等压变化,
T1=273+27=300K,V1=LS,V2=2LS,
由盖吕萨克定律得:$\frac{{V}_{1}}{{T}_{1}}$=$\frac{{V}_{2}}{{T}_{2}}$,即:$\frac{LS}{300}$=$\frac{2LS}{{T}_{2}}$,
解得:T2=600K;
(2)气体体积不变,气体发生等容变化,
p2=p0=1×105Pa,T2=600K,T3=273+27=300K,
由查理定律得:$\frac{{p}_{2}}{{T}_{2}}$=$\frac{{p}_{3}}{{T}_{3}}$,即:$\frac{1×1{0}^{5}}{600}$=$\frac{{p}_{3}}{300}$,
解得:p3=5×104Pa,
气体压强P随温度T变化的图象如图所示: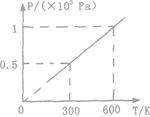
答:(1)当活塞到达M′N′后气体的温度为600K;
(2)气体的压强是5×104Pa,图象如图所示.
点评 本题考查了求气体的温度、气体压强,首先确定气体的状态变化过程,应用盖吕萨克定律与查理定律即可正确解题,求出气体的状态参量是正确解题的关键.

练习册系列答案
相关题目
5. 2014年春晚中开心麻花团队打造的创意形体秀《魔幻三兄弟》给观众留下了很深的印象.该剧采用了“斜躺”的表演方式,三位演员躺在倾角为30°的斜面上完成一系列动作,摄像机垂直于斜面拍摄,让观众产生演员在竖直墙面前表演的错觉.如图所示,演员甲被演员乙和演员丙“竖直向上”抛出,到最高点后恰好悬停在“空中”.已知演员甲的质量m=60kg,该过程中观众看到演员甲上升的“高度”为0.8m.设演员甲和斜面间最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2,不计空气阻力.则该过程中,下列说法正确的是( )
2014年春晚中开心麻花团队打造的创意形体秀《魔幻三兄弟》给观众留下了很深的印象.该剧采用了“斜躺”的表演方式,三位演员躺在倾角为30°的斜面上完成一系列动作,摄像机垂直于斜面拍摄,让观众产生演员在竖直墙面前表演的错觉.如图所示,演员甲被演员乙和演员丙“竖直向上”抛出,到最高点后恰好悬停在“空中”.已知演员甲的质量m=60kg,该过程中观众看到演员甲上升的“高度”为0.8m.设演员甲和斜面间最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2,不计空气阻力.则该过程中,下列说法正确的是( )
 2014年春晚中开心麻花团队打造的创意形体秀《魔幻三兄弟》给观众留下了很深的印象.该剧采用了“斜躺”的表演方式,三位演员躺在倾角为30°的斜面上完成一系列动作,摄像机垂直于斜面拍摄,让观众产生演员在竖直墙面前表演的错觉.如图所示,演员甲被演员乙和演员丙“竖直向上”抛出,到最高点后恰好悬停在“空中”.已知演员甲的质量m=60kg,该过程中观众看到演员甲上升的“高度”为0.8m.设演员甲和斜面间最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2,不计空气阻力.则该过程中,下列说法正确的是( )
2014年春晚中开心麻花团队打造的创意形体秀《魔幻三兄弟》给观众留下了很深的印象.该剧采用了“斜躺”的表演方式,三位演员躺在倾角为30°的斜面上完成一系列动作,摄像机垂直于斜面拍摄,让观众产生演员在竖直墙面前表演的错觉.如图所示,演员甲被演员乙和演员丙“竖直向上”抛出,到最高点后恰好悬停在“空中”.已知演员甲的质量m=60kg,该过程中观众看到演员甲上升的“高度”为0.8m.设演员甲和斜面间最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2,不计空气阻力.则该过程中,下列说法正确的是( )| A. | 演员甲被抛出的初速度为4m/s | B. | 演员甲运动的时间为0.8s | ||
| C. | 演员乙和演员丙对甲做的功为480J | D. | 演员甲的重力势能增加了480J |
2.如图,电源为“9V 1Ω”的电池组要将“4V 4W”的灯泡接人虚线框中,在正常发光的条件下,最多能接( )
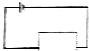

| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9.最先揭示了电现象和磁现象之间存在着某种联系,发现了电流的磁效应的学者是( )
| A. | 安培 | B. | 法拉第 | C. | 奥斯特 | D. | 库伦 |
6.以相同初速度先后从同一位置竖直上抛甲、乙两个小球,不计空气阻力,它们在空中相遇时具有相同的( )
| A. | 加速度 | B. | 速度 | ||
| C. | 平均速度 | D. | 位移(相对于抛出点) |
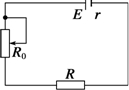 如图所示的电路中.电池的电动势E=5v,内电阻r=10Ω,固定电阻R=90Ω,R0是可变电阻,在R0由0增加到400Ω的过程中,求:
如图所示的电路中.电池的电动势E=5v,内电阻r=10Ω,固定电阻R=90Ω,R0是可变电阻,在R0由0增加到400Ω的过程中,求: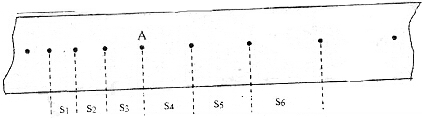 如图所示,某同学在做“研究匀变速直线运动”试验中,由打点计时器得到表示小车运动的一条纸带,纸带上相邻计数点的时间间隔为T=0.10s,各间距S1=7.05cm,S2=7.687cm,S3=8.33cm,S4=8.95cm,S5=9.61cm,S6=10.26cm,则A处瞬时速度的大小为0.864,小车运动加速度的表达式为$\frac{({s}_{4}+{s}_{5}+{s}_{6})-({s}_{1}+{s}_{2}+{s}_{3})}{9{T}^{2}}$,加速度的大小为0.639.(以上计算结果均保留三位有效数字)
如图所示,某同学在做“研究匀变速直线运动”试验中,由打点计时器得到表示小车运动的一条纸带,纸带上相邻计数点的时间间隔为T=0.10s,各间距S1=7.05cm,S2=7.687cm,S3=8.33cm,S4=8.95cm,S5=9.61cm,S6=10.26cm,则A处瞬时速度的大小为0.864,小车运动加速度的表达式为$\frac{({s}_{4}+{s}_{5}+{s}_{6})-({s}_{1}+{s}_{2}+{s}_{3})}{9{T}^{2}}$,加速度的大小为0.639.(以上计算结果均保留三位有效数字) 如图所示,竖直放置的U形管,左端封闭右端开口,管内水银将长19cm的空气柱封在左管内,此时两管内水银面的高度差为4cm,大气压强为标准大气压75mmHg.现向右管内再注入水银,使空气柱长度减少1cm,若温度保持不变,则需注入水银柱的长度为多少?
如图所示,竖直放置的U形管,左端封闭右端开口,管内水银将长19cm的空气柱封在左管内,此时两管内水银面的高度差为4cm,大气压强为标准大气压75mmHg.现向右管内再注入水银,使空气柱长度减少1cm,若温度保持不变,则需注入水银柱的长度为多少?