题目内容
某学校科技兴趣小组,利用废旧物品制作了一个简易气温计:在一个空葡萄酒瓶中插入一根两端开口的玻璃管,玻璃管内有一段长度可忽略的水银柱,接口处用蜡密封,将酒瓶水平放置,如图所示.已知:该装置密封气体的体积为560cm3,玻璃管内部横截面积为0.5cm2,瓶口外的有效长度为48cm.当气温为7℃时,水银柱刚好处在瓶口位置.(1)求该气温计能测量的最高气温.
(2)假设水银柱从瓶口处缓慢移动到最右端的过程中,密封气体从外界吸收3.2J热量,问在这一过程中该气体的内能如何变化?变化了多少?(已知大气压为1×105Pa)

【答案】分析:(1)玻璃管两端开口,水银柱移动时,密封的气体发生等压变化,当水银柱到达管口时,所测气温最高,根据吕萨克定律求解.
(2)由热力学第一定律△U=W+Q,分析吸放热.
解答:解:(1)当水银柱到达管口时,所测气温最高,设为T2,此时气体体积为V2,
初状态:T1=(273+7)K=280K; V1=560cm3,末状态V2=(560+48×0.5)cm3=584cm3,
气体发生等压变化,由概率萨克定律得: =
= ,即:
,即: =
= ,
,
解得:T2=292K;
(2)水银柱移动过程中,外界对气体做功W=-PSL=-1×105×0.5×10-4×48×10-2J=-2.4J,
由热力学第一定律知内能变化为:△U=W+Q=-2.4J+3.2J=0.8J,气体内能增加;
答:(1)该气温计能测量的最高气温是292K;
(2)气体内能增加,增加了0.8J.
点评:对于气体状态变化问题,关键在于分析是等值变化还是三个参量同时变化的问题,要善于挖掘隐含的条件.
(2)由热力学第一定律△U=W+Q,分析吸放热.
解答:解:(1)当水银柱到达管口时,所测气温最高,设为T2,此时气体体积为V2,
初状态:T1=(273+7)K=280K; V1=560cm3,末状态V2=(560+48×0.5)cm3=584cm3,
气体发生等压变化,由概率萨克定律得:
 =
= ,即:
,即: =
= ,
,解得:T2=292K;
(2)水银柱移动过程中,外界对气体做功W=-PSL=-1×105×0.5×10-4×48×10-2J=-2.4J,
由热力学第一定律知内能变化为:△U=W+Q=-2.4J+3.2J=0.8J,气体内能增加;
答:(1)该气温计能测量的最高气温是292K;
(2)气体内能增加,增加了0.8J.
点评:对于气体状态变化问题,关键在于分析是等值变化还是三个参量同时变化的问题,要善于挖掘隐含的条件.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
 (2010?临沂一模)某学校科技兴趣小组,利用废旧物品制作了一个简易气温计:在一个空葡萄酒瓶中插入一根两端开口的玻璃管,玻璃管内有一段长度可忽略的水银柱,接口处用蜡密封,将酒瓶水平放置,如图所示.已知:该装置密封气体的体积为480cm3,玻璃管内部横截面积为0.4cm2,瓶口外的有效长度为48cm.当气温为7°C时,水银柱刚好处在瓶口位置.
(2010?临沂一模)某学校科技兴趣小组,利用废旧物品制作了一个简易气温计:在一个空葡萄酒瓶中插入一根两端开口的玻璃管,玻璃管内有一段长度可忽略的水银柱,接口处用蜡密封,将酒瓶水平放置,如图所示.已知:该装置密封气体的体积为480cm3,玻璃管内部横截面积为0.4cm2,瓶口外的有效长度为48cm.当气温为7°C时,水银柱刚好处在瓶口位置. 某学校科技兴趣小组,利用废旧物品制作了一个简易气温计:在一个空葡萄酒瓶中插入一根两端开口的玻璃管,玻璃管内有一段长度可忽略的水银柱,接口处用蜡密封,将酒瓶水平放置,如图所示.已知:该装置密封气体的体积为560cm3,玻璃管内部横截面积为0.5cm2,瓶口外的有效长度为48cm.当气温为7℃时,水银柱刚好处在瓶口位置.
某学校科技兴趣小组,利用废旧物品制作了一个简易气温计:在一个空葡萄酒瓶中插入一根两端开口的玻璃管,玻璃管内有一段长度可忽略的水银柱,接口处用蜡密封,将酒瓶水平放置,如图所示.已知:该装置密封气体的体积为560cm3,玻璃管内部横截面积为0.5cm2,瓶口外的有效长度为48cm.当气温为7℃时,水银柱刚好处在瓶口位置.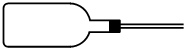 [物理-物理3-3]
[物理-物理3-3]
