题目内容
（11分）如图所示，水平地面AB=10m．BCD是半径为R=0．9m的光滑半圆轨道，O是圆心，DOB在同一竖直线上．一个质量m=1．0kg的物体静止在A点．现用F=10N的水平恒力作用在物体上，使物体从静止开始做匀加速直线运动．物体与水平地面间的动摩擦因数μ=0．5．当物体运动到B点时撤去F，以后物体沿BCD轨道运动，离开最高点D后落到地上的P点（图中未画出）．g取10 m/s2．求：
?（1）物体运动到B点时的速度大小vB；；
?（2）物体运动到D点时的速度大小vD；；
?（3）物体落地点P与B点间的距离
解：（1）物体从A到B，根据动能定理
（F-f）s=
mvB2 （1分）
f=μmg （1分）
代入数据求出vB=10m/s． （1分）
（2）从B到D，由机械能守恒定律mvB2=mg·2R+mvD2 （2分）
求出vD=8m/s． （1分）
（3）物体离开D点后做平抛运动 竖直方向：2R=gt2 （2分）
水平方向：PB=vDt? （2分）
求出PB=4．8m． （1分）
练习册系列答案
名校课堂系列答案
相关题目
如图所示，水平地面上方分布着水平向右的匀强电场，一个“L”形的绝缘硬质粗细均匀细管AOB竖直固定在匀强电场中，管的水平部分长为L1=0.20m且离水平面地面的高度为h=5.0m，AO⊥OB，竖直管部分长为L2=0.10m，一带正电的小球（直径略小于细管内径）从管的上端入口A处由静止释放，小球与管壁间摩擦不计，小球通过弯管（极短的弯折部分）时没有能量损失，小球所在的空间电场强度为E=mg/2q．求：（g=10m/s2） 
（2011?江西模拟）如图所示，水平地面上方矩形区域内存在垂直纸面向里的匀强磁场，两个边长不等的单匝闭合正方形线圈Ⅰ和Ⅱ，分别用相同材料，不同粗细的导线绕制（Ⅰ为边长短的细导线）．两线圈的下边距磁场上界面高度相同，同由静止开始自由下落，再进入磁场，最后落到地面．运动过程中，线圈平面始终保持在竖直平面内且下边缘平行于磁场上边界．设线圈Ⅰ、Ⅱ落地时的速度大小分别为v1、v2，运动时间分别为t1、t2 在磁场中运动时产生的热量分别为Q1、Q2．不计空气阻力，则（ ）
如图所示，水平地面上方分布着水平向右的匀强电场．一“L”形的由绝缘材料制成的硬质管竖直固定在匀强电场中．管的水平部分长为l1=0.2m，管的水平部分离水平地面的距离为h=5.0m，竖直部分长为l2=0.1m．一带正电的小球a从管口A由静止释放，小球与管间摩擦不计且小球通过管的弯曲部分（长度极短可不计）时没有机械能损失，小球在电场中受到的电场力大小为重力的一半．一个与小球a质量相同且不带电的小球b静止在管口B处，当小球运动到管口B时与小球b 相碰并粘在一起（g=10m/s2）求：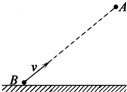
如图所示，水平地面附近，小球B以初速度v斜向上瞄准另一小球A射出，恰巧在B球射出的同时，A球由静止开始下落，不计空气阻力．则两球在空中运动的过程中（ ）
如图所示，水平地面AB与倾角为θ的斜面平滑相连．一个质量为m的物块静止在A点．现用水平恒力F作用在物块上，使物块从静止开始做匀加速直线运动，经时间t到达B点，此时撤去力F，物块以在B点的速度大小冲上斜面，并最终又返回到水平面停下．已知物块与水平地面和斜面间的动摩擦因数均为μ，重力加速度为g．求：