题目内容
5. 如图所示,倾角θ=30°的光滑斜面上的P点距水平面高h=0.2m,滑块A自P点由静止释放,同时滑块B自水平面上的Q点以速度v0=5m/s向右运动,已知B与水平面间的动摩擦因数μ=0.4,滑块A与滑块B材料相同,滑块A释放后经过t=1s在水平面上刚好与滑块B相遇.假设滑块A滑过O点时机械能不损失.g取10m/s2,两滑块均可视为质点.求:Q点与斜面底端O点的距离.
如图所示,倾角θ=30°的光滑斜面上的P点距水平面高h=0.2m,滑块A自P点由静止释放,同时滑块B自水平面上的Q点以速度v0=5m/s向右运动,已知B与水平面间的动摩擦因数μ=0.4,滑块A与滑块B材料相同,滑块A释放后经过t=1s在水平面上刚好与滑块B相遇.假设滑块A滑过O点时机械能不损失.g取10m/s2,两滑块均可视为质点.求:Q点与斜面底端O点的距离.
分析 根据牛顿第二定律和运动学公式求出A在斜面上运动的时间,以及运动到O处时的速度;两物体在水平面上做减速运动,据时间关系和位移关系求出Q点到O点的距离即可.
解答 解:从P到O,根据动能定理得,mgh=$\frac{1}{2}m{{v}_{1}}^{2}$,
解得${v}_{1}=\sqrt{2gh}=\sqrt{2×10×0.2}$m/s=2m/s.
根据牛顿第二定律知,在斜面上的加速度${a}_{1}=gsinθ=10×\frac{1}{2}m/{s}^{2}=5m/{s}^{2}$,
则A滑动底端的时间${t}_{1}=\frac{{v}_{1}}{{a}_{1}}=\frac{2}{5}s=0.4s$,
在水平面上的加速度大小${a}_{2}=μg=0.4×10m/{s}^{2}=4m/{s}^{2}$,
A在水平面上速度减为零的时间${t}_{2}=\frac{{v}_{1}}{{a}_{2}}=\frac{2}{4}s=0.5s$,
A物体运动0.9s之后静止,B物体运动1s后与A相碰,${x}_{A}=\frac{{{v}_{1}}^{2}}{2{a}_{2}}=\frac{4}{8}m=0.5m$,
B物体一直做匀减速运动,${x}_{B}={v}_{0}t-\frac{1}{2}{a}_{2}{t}^{2}=5×1-\frac{1}{2}×4×1m=3m$,
则d=xA+xB=3.5m.
答:Q点与斜面底端O点的距离为3.5m.
点评 分析清楚AB两物体的运动情况是解题的关键,灵活应用时间和位移关系是解题的核心,注意匀减速直线运动判断是否停下来,此题难度较大.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
15.如图所示,弹簧振子沿x轴在B、C之间做简谐运动,O为平衡位置,当振子从B点向O点运动经过点P时( )
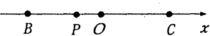
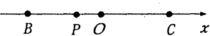
| A. | 振子的位移为负 | B. | 振子的加速度为负 | ||
| C. | 振子的速度为负 | D. | 振子的回复力为负 |
20. 双人滑运动员在光滑的水平冰面上做表演,甲运动员给乙运动员一个水平恒力F,乙运动员在冰面上完成了一段优美的弧线MN.vM与vN正好成90°角,则此过程中,乙运动员受到甲运动员的恒力可能是图中的( )
双人滑运动员在光滑的水平冰面上做表演,甲运动员给乙运动员一个水平恒力F,乙运动员在冰面上完成了一段优美的弧线MN.vM与vN正好成90°角,则此过程中,乙运动员受到甲运动员的恒力可能是图中的( )
 双人滑运动员在光滑的水平冰面上做表演,甲运动员给乙运动员一个水平恒力F,乙运动员在冰面上完成了一段优美的弧线MN.vM与vN正好成90°角,则此过程中,乙运动员受到甲运动员的恒力可能是图中的( )
双人滑运动员在光滑的水平冰面上做表演,甲运动员给乙运动员一个水平恒力F,乙运动员在冰面上完成了一段优美的弧线MN.vM与vN正好成90°角,则此过程中,乙运动员受到甲运动员的恒力可能是图中的( )| A. | F1 | B. | F2 | C. | F3 | D. | F4 |
10.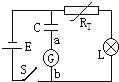 如图所示.E为电源,其内电阻不可忽略,RT为热敏电阻,其阻值随温度升高而减小,L为指示灯泡,C为平行板电容器,G为灵敏电流计.闭合开关S,当环境的温度明显升高时,下列说法正确的是( )
如图所示.E为电源,其内电阻不可忽略,RT为热敏电阻,其阻值随温度升高而减小,L为指示灯泡,C为平行板电容器,G为灵敏电流计.闭合开关S,当环境的温度明显升高时,下列说法正确的是( )
 如图所示.E为电源,其内电阻不可忽略,RT为热敏电阻,其阻值随温度升高而减小,L为指示灯泡,C为平行板电容器,G为灵敏电流计.闭合开关S,当环境的温度明显升高时,下列说法正确的是( )
如图所示.E为电源,其内电阻不可忽略,RT为热敏电阻,其阻值随温度升高而减小,L为指示灯泡,C为平行板电容器,G为灵敏电流计.闭合开关S,当环境的温度明显升高时,下列说法正确的是( )| A. | 灯泡L变亮 | B. | 热敏电阻RT两端电压变大 | ||
| C. | 电容器C所带电荷量保持不变 | D. | 电流计G中电流方向由a到b |
17.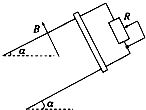 如图所示,光滑平行的足够长金属导轨与水平方向成α=30°角,导轨的宽度为0.5m,R为滑动变阻器,空间有垂直于导轨平面的匀强磁场,磁感应强度的大小B=1T.一根质量m=1kg,内阻r=1Ω的金属杆从导轨上端由静止滑下,经过足够长的时间后,金属杆的速度达到最大值vm.已知重力加速度g=10m/s2,不计导轨电阻.关于金属杆最大速度的范围下列说法正确的是( )
如图所示,光滑平行的足够长金属导轨与水平方向成α=30°角,导轨的宽度为0.5m,R为滑动变阻器,空间有垂直于导轨平面的匀强磁场,磁感应强度的大小B=1T.一根质量m=1kg,内阻r=1Ω的金属杆从导轨上端由静止滑下,经过足够长的时间后,金属杆的速度达到最大值vm.已知重力加速度g=10m/s2,不计导轨电阻.关于金属杆最大速度的范围下列说法正确的是( )
 如图所示,光滑平行的足够长金属导轨与水平方向成α=30°角,导轨的宽度为0.5m,R为滑动变阻器,空间有垂直于导轨平面的匀强磁场,磁感应强度的大小B=1T.一根质量m=1kg,内阻r=1Ω的金属杆从导轨上端由静止滑下,经过足够长的时间后,金属杆的速度达到最大值vm.已知重力加速度g=10m/s2,不计导轨电阻.关于金属杆最大速度的范围下列说法正确的是( )
如图所示,光滑平行的足够长金属导轨与水平方向成α=30°角,导轨的宽度为0.5m,R为滑动变阻器,空间有垂直于导轨平面的匀强磁场,磁感应强度的大小B=1T.一根质量m=1kg,内阻r=1Ω的金属杆从导轨上端由静止滑下,经过足够长的时间后,金属杆的速度达到最大值vm.已知重力加速度g=10m/s2,不计导轨电阻.关于金属杆最大速度的范围下列说法正确的是( )| A. | vm≥20m/s | B. | 0m/s<vm<15m/s | C. | 0m/s<vm<20m/s | D. | 15m/s<vm<20m/s |
14.在学习光的色散的时候老师课堂上做了一个演示实验,让某特制的一束复色光由空气射入一块平行平面玻璃砖(玻璃较厚),经折射分成两束单色光a、b,已知a光是红光,而b光是蓝光,下列光路图正确的是( )
| A. | 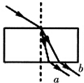 | B. | 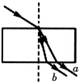 | C. | 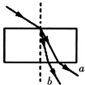 | D. | 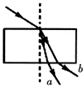 |
15.关于重力势能的几种理解,正确的是( )
| A. | 重力势能等于零的物体,一定不会对别的物体做功 | |
| B. | 相对于不同的参考平面物体其有不同数值的重力势能,但这并不影响研究有关重力势能的问题 | |
| C. | 在同一高度将物体不论向任何方向抛出.只要抛出时的初速度大小相同,则落地时减少的重力势能必相等 | |
| D. | 放在地面的物体,它的重力势能一定等于零 |
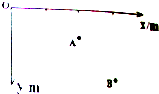 在如图所示的xOy直角坐标系(y轴正向为竖直向下)中,有A、B两点.A点坐标为(2,0.8),B点的坐标为(3,2).将一个球从O点以速度v0沿x轴正向抛出,恰好能经过A点,不计空气阻力,取g=10m/s2.求:
在如图所示的xOy直角坐标系(y轴正向为竖直向下)中,有A、B两点.A点坐标为(2,0.8),B点的坐标为(3,2).将一个球从O点以速度v0沿x轴正向抛出,恰好能经过A点,不计空气阻力,取g=10m/s2.求: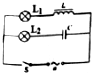 如图所示电路,L1和L2是两个相同的白炽灯,交流电源的电压最大值为Um,频率为f时,两灯的亮度相同,现在保持电压最大值Um不变,而频率为f增大,则L1的亮度减弱(填“增加”或“减弱”),L2的亮度增加(填“增加”或“减少”)
如图所示电路,L1和L2是两个相同的白炽灯,交流电源的电压最大值为Um,频率为f时,两灯的亮度相同,现在保持电压最大值Um不变,而频率为f增大,则L1的亮度减弱(填“增加”或“减弱”),L2的亮度增加(填“增加”或“减少”)