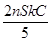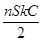题目内容
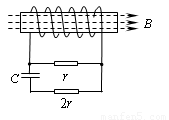
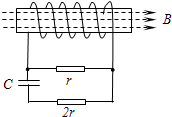 如图所示,线圈匝数为n,横截面积为S,线圈电阻为r,处于一个均匀增强的磁场中,磁感应强度随时间的变化率为k,磁场方向水平向右且与线圈平面垂直,电容器的电容为C,两个电阻的阻值分别为r和2r.由此可知,下列说法正确的是( )
如图所示,线圈匝数为n,横截面积为S,线圈电阻为r,处于一个均匀增强的磁场中,磁感应强度随时间的变化率为k,磁场方向水平向右且与线圈平面垂直,电容器的电容为C,两个电阻的阻值分别为r和2r.由此可知,下列说法正确的是( )A、电容器所带电荷量为
| ||
B、电容器所带电荷量为
| ||
| C、电容器下极板带正电 | ||
| D、电容器上极板带正电 |
分析:磁场均匀增强,线圈中产生恒定的感应电动势,相当于电源.根据法拉第定律可求得感应电动势的大小,由电路的结构求出路端电压.带电微粒P处于平衡状态,电场力与重力平衡,由平衡条件列式,即可求出P的电荷量,由楞次定律判断电容器极板的电性,从而判断P的电性.
解答:解:AB、闭合线圈与阻值为r的电阻形成闭合回路,线圈相当与电源,电容器两极板间的电压等于路端电压,
线圈产生的感应电动势为:E=nS
=nSk,
路端电压:U=
?r=
,
则电容器所带电荷量为:Q=CU=
,故AB错误;
CD、根据磁场向右均匀增强,并由楞次定律可知,电容器上极板带正电,故C错误,D正确.
故选:D.
线圈产生的感应电动势为:E=nS
| △ B |
| △t |
路端电压:U=
| E |
| 2r |
| E |
| 2 |
则电容器所带电荷量为:Q=CU=
| nSkC |
| 2 |
CD、根据磁场向右均匀增强,并由楞次定律可知,电容器上极板带正电,故C错误,D正确.
故选:D.
点评:本题是电磁感应与带电粒子在电场平衡问题的综合,关键要能根据法拉第定律求出感应电动势,由楞次定律判断感应电动势的方向.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
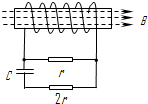 如图所示,线圈匝数为n,横截面积为S,线圈电阻为r,处于一个均匀增强的磁场中,磁感应强度随时间的变化率为k,磁场方向水平向右且与线圈平面垂直,电容器的电容为C,两个电阻的阻值分别为r和2r.由此可知,下列说法正确的是( )
如图所示,线圈匝数为n,横截面积为S,线圈电阻为r,处于一个均匀增强的磁场中,磁感应强度随时间的变化率为k,磁场方向水平向右且与线圈平面垂直,电容器的电容为C,两个电阻的阻值分别为r和2r.由此可知,下列说法正确的是( )| A、电容器上极板带正电 | ||
| B、电容器下极板带正电 | ||
C、电容器所带电荷量为
| ||
D、电容器所带电荷量为
|
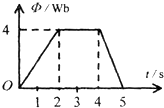 穿过单匝线圈的磁通量Φ随时间t变化情况如图所示,线圈匝数为20匝,则线圈内的感应电动势的最大值是
穿过单匝线圈的磁通量Φ随时间t变化情况如图所示,线圈匝数为20匝,则线圈内的感应电动势的最大值是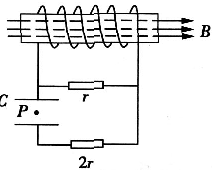 如图所示,线圈匝数为n,横截面积为S,线圈电阻为r,处于一个均匀增强的磁场中,磁感应强度随时间的变化率为k(k>0),磁场方向水平向右且与线圈平面垂直.上、下两板水平放置的电容器,板间距为d,电容为C,在电容器两板之间有一质量为m的带电微粒P处于静止状态,两个电阻的阻值分别为r和2r.则下列说法正确的是( )
如图所示,线圈匝数为n,横截面积为S,线圈电阻为r,处于一个均匀增强的磁场中,磁感应强度随时间的变化率为k(k>0),磁场方向水平向右且与线圈平面垂直.上、下两板水平放置的电容器,板间距为d,电容为C,在电容器两板之间有一质量为m的带电微粒P处于静止状态,两个电阻的阻值分别为r和2r.则下列说法正确的是( )