题目内容
15. 在探究弹力和弹簧伸长量的关系时,某同学先按图1对弹簧甲进行探究,然后将弹簧乙和弹簧甲串联起来按图2进行探究.不考虑两个弹簧重力的影响,在弹性限度内,将质量m=50g的钩码逐个挂在弹簧下端,分别测得图1、图2中弹簧总长度L1、L2如表所示.取g=9.8m/s2,则弹簧甲的劲度系数k甲=100N/m,弹簧乙的劲度系数k乙=50N/m.
在探究弹力和弹簧伸长量的关系时,某同学先按图1对弹簧甲进行探究,然后将弹簧乙和弹簧甲串联起来按图2进行探究.不考虑两个弹簧重力的影响,在弹性限度内,将质量m=50g的钩码逐个挂在弹簧下端,分别测得图1、图2中弹簧总长度L1、L2如表所示.取g=9.8m/s2,则弹簧甲的劲度系数k甲=100N/m,弹簧乙的劲度系数k乙=50N/m.| 钩码个数 | 1 | 2 | 3 | 4 |
| L1/cm | 26.00 | 26.48 | 26.97 | 27.47 |
| L2/cm | 79.44 | 80.89 | 82.36 | 83.85 |
分析 根据弹簧形变量的变化量,结合胡克定律求出弹簧甲的劲度系数.通过弹簧并联时的弹力的变化量和形变量的变化量可以求出弹簧并联的劲度系数.
解答 解:由表格中的数据可知,当弹力的变化量△F=2mg=2×0.05×9.8N=0.98N时,
弹簧形变量的变化量为△x1=$\frac{(26.97-26.00)+(27.47-26.48)}{2}$=0.98cm,
根据胡克定律知甲的劲度系数:k1=$\frac{△F}{△x}$=$\frac{0.98}{0.0098}$=100N/m.
根据表中数据要知,乙的形变量分别为53.44cm、54.41cm、55.39cm、56.38cm;
同理可解得k2=$\frac{0.98}{0.0196}$=50N/m;故
答案为:100 50
点评 解决本题的关键掌握胡克定律,知道F=kx,x表示形变量,以及知道其变形式△F=k△x,△x为形变量的变化量.

练习册系列答案
相关题目
5. 表面光滑、半径为R的半球固定在水平地面上,球心O的正上方O′处有一无摩擦定滑轮,轻质细绳两端各系一个小球挂在定滑轮上,如图所示.两小球平衡时,若滑轮两侧细绳的长度分别为L1=2.4R和L2=2.5R,则这两个小球的质量之比m1:m2为(不计球的大小)( )
表面光滑、半径为R的半球固定在水平地面上,球心O的正上方O′处有一无摩擦定滑轮,轻质细绳两端各系一个小球挂在定滑轮上,如图所示.两小球平衡时,若滑轮两侧细绳的长度分别为L1=2.4R和L2=2.5R,则这两个小球的质量之比m1:m2为(不计球的大小)( )
 表面光滑、半径为R的半球固定在水平地面上,球心O的正上方O′处有一无摩擦定滑轮,轻质细绳两端各系一个小球挂在定滑轮上,如图所示.两小球平衡时,若滑轮两侧细绳的长度分别为L1=2.4R和L2=2.5R,则这两个小球的质量之比m1:m2为(不计球的大小)( )
表面光滑、半径为R的半球固定在水平地面上,球心O的正上方O′处有一无摩擦定滑轮,轻质细绳两端各系一个小球挂在定滑轮上,如图所示.两小球平衡时,若滑轮两侧细绳的长度分别为L1=2.4R和L2=2.5R,则这两个小球的质量之比m1:m2为(不计球的大小)( )| A. | 24:1 | B. | 25:1 | C. | 24:25 | D. | 25:24 |
6.如图,物体沿光滑曲面滑下,不计空气阻力,下列说法正确的是( )
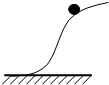

| A. | 物体机械能增大 | |
| B. | 物体重力势能增加,动能增加 | |
| C. | 重力对物体做负功 | |
| D. | 重力对物体做的功等于物体动能的增加 |
10.(多选)如图所示为沿同一直线上运动的A、B两个人(可以看作质点)的x-t图象,由图可知( )


| A. | t=0时刻,A在B的前面 | |
| B. | 0-t2这段时间内A运动的速度始终比B大 | |
| C. | B开始运动的速度比A小,t2时刻后才大于A的速度 | |
| D. | B在t2时刻追上A,并在此后跑在A的前面 |
7.如图所示,一个弹簧振子在A、B两点间做简谐运动,O点为平衡位置,下列说法中正确的有( )
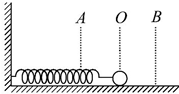

| A. | 它在A、B两点时动能为零 | |
| B. | 它经过O点时加速度方向不发生变化 | |
| C. | 它远离O点时做匀减速运动 | |
| D. | 它所受回复力的方向总跟它偏离平衡位置的位移方向相反 |
5.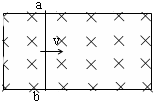 如图,垂直矩形金属框的匀强磁场磁感应强度为B,长为L的导体棒ab垂直线框两长边放在框上(线框的宽也为L),在△t时间内,ab向右匀速滑过距离d,则( )
如图,垂直矩形金属框的匀强磁场磁感应强度为B,长为L的导体棒ab垂直线框两长边放在框上(线框的宽也为L),在△t时间内,ab向右匀速滑过距离d,则( )
 如图,垂直矩形金属框的匀强磁场磁感应强度为B,长为L的导体棒ab垂直线框两长边放在框上(线框的宽也为L),在△t时间内,ab向右匀速滑过距离d,则( )
如图,垂直矩形金属框的匀强磁场磁感应强度为B,长为L的导体棒ab垂直线框两长边放在框上(线框的宽也为L),在△t时间内,ab向右匀速滑过距离d,则( )| A. | 右边减少d,左边增加d,则△φ=B2Ld,ε=$\frac{{B}^{2}Ld}{△t}$ | |
| B. | 右边减少d,左边增加d,两边抵消,△φ=0,ε=0 | |
| C. | 不能用ε=$\frac{△φ}{△t}$计算,只能用ε=BLv | |
| D. | △φ=BLd,ε=$\frac{△φ}{△t}$=$\frac{BLd}{△t}$ |
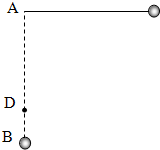 如图所示,质量为m的小球,由长为R的细线系住,细线的另一端固定在A点,AB是过A的竖直线,在AB上钉铁钉D,线能承受的最大拉力是10mg(g为重力加速度),现将细线沿水平方向拉直,然后由静止释放,不计线与钉子碰撞时的能量损失,不计空气阻力,求:
如图所示,质量为m的小球,由长为R的细线系住,细线的另一端固定在A点,AB是过A的竖直线,在AB上钉铁钉D,线能承受的最大拉力是10mg(g为重力加速度),现将细线沿水平方向拉直,然后由静止释放,不计线与钉子碰撞时的能量损失,不计空气阻力,求: 验证牛顿第二定律的实验装置如图所示,在水平桌面上放置一带有定滑轮的长木板,将光电门固定在长木板上的B点.小车上端固定宽度为d的遮光条,前端固定力传感器,一物体通过细线跨过定滑轮与力传感器相连,这样传感器就可测出细线拉力的大小.每次小车都从同一位置A由静止释放,已知A、B间的距离为L.改变小车上砝码个数,测出小车的质量M(含砝码、传感器与遮光条),记录对应传感器的示数F和遮光条通过光电门的时间△t.
验证牛顿第二定律的实验装置如图所示,在水平桌面上放置一带有定滑轮的长木板,将光电门固定在长木板上的B点.小车上端固定宽度为d的遮光条,前端固定力传感器,一物体通过细线跨过定滑轮与力传感器相连,这样传感器就可测出细线拉力的大小.每次小车都从同一位置A由静止释放,已知A、B间的距离为L.改变小车上砝码个数,测出小车的质量M(含砝码、传感器与遮光条),记录对应传感器的示数F和遮光条通过光电门的时间△t.