Question

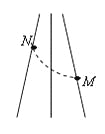
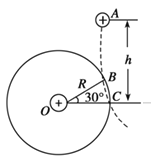
【题目】如图所示，在竖直平面内，用长为L的绝缘轻绳将质量为m、带电量为的小球悬于O点，整个装置处在水平向右的匀强电场中。初始时刻小球静止在P点。细绳与场强方向成角。今用绝缘锤子沿竖直平面、垂直于OP方向打击一下小球，之后迅速撤离锤子，当小球回到P处时，再次用锤子沿同一方向打击小球，两次打击小球恰好到达Q点，且小球始终未脱离圆周轨道，打击的时间极短，小球电荷量不损失。锤子第一次对小球做功为，第二次对球做功为。

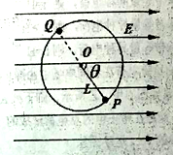
（1）求匀强电场的场强大小E；

（2）若的值达到最大，分别求、；

（3）的值最大时，求第一、二次小球被打击后瞬间细绳的拉力大小、。

Answer 1

【答案】（1）;（2），；

（3），

【解析】

试题分析：（1）如图所示，在A点合力为零，则，则。

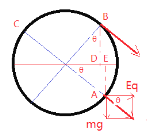
（2）第一次击打后球最多到达“等效”与球心等高B位置，根据功能关系，有：

在等效最高点C时，根据牛顿第二定律：

根据功能关系：

整理可以得到：

整理可以得到：，。

（3）打击一次后，物体获得的速度为，则

根据牛顿第二定律：

打击二次后，物体获得的速度为，则

根据牛顿第二定律：

联立整理可以得到：，。