题目内容
7.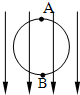 有一匀强电场,其场强为E,方向竖直向下.把一个半径为r的光滑绝缘环,竖直置于电场中,环面平行于电场线,环的顶点A穿有一个质量为m、电量为q(q>0)的空心小球,如图所示.当小球由静止开始从A点下滑到最低点B时,小球的速度大小是多少?小球受到环的支持力多大?
有一匀强电场,其场强为E,方向竖直向下.把一个半径为r的光滑绝缘环,竖直置于电场中,环面平行于电场线,环的顶点A穿有一个质量为m、电量为q(q>0)的空心小球,如图所示.当小球由静止开始从A点下滑到最低点B时,小球的速度大小是多少?小球受到环的支持力多大?
分析 设小球到达B点时的速度为v,由动能定理列式求v.在B点处由牛顿第二定律列式,联立方程组即可求解小球受到环的支持力.
解答 解:设小球到达B点时的速度为v,由动能定理得
(mg+qE)•2r=$\frac{1}{2}$mv2
解之得 v=2$\sqrt{\frac{(mg+qE)r}{m}}$…①
在B点处由牛顿第二定律得
N-mg-qE=m$\frac{{v}^{2}}{r}$…②
联立①和②式,解得小球在B点受到环的压力为:N=5(mg+qE)
答:当小球由静止开始从A点下滑到最低点B时,小球的速度大小是2$\sqrt{\frac{(mg+qE)r}{m}}$,小球受到环的支持力是5(mg+qE).
点评 本题主要考查了动能定理及牛顿第二定律的直接应用,关键要正确分析小球的受力情况和做功情况,注意是在B点,由合外力提供向心力.

练习册系列答案
相关题目
18. 一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持以额定功率运动.其v-t图象如图所示.已知汽车的质量为m=1×103kg,汽车受到地面的阻力为车重的0.1倍,则以下说法正确的是( )
一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持以额定功率运动.其v-t图象如图所示.已知汽车的质量为m=1×103kg,汽车受到地面的阻力为车重的0.1倍,则以下说法正确的是( )
 一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持以额定功率运动.其v-t图象如图所示.已知汽车的质量为m=1×103kg,汽车受到地面的阻力为车重的0.1倍,则以下说法正确的是( )
一辆小汽车在水平路面上由静止启动,在前5s内做匀加速直线运动,5s末达到额定功率,之后保持以额定功率运动.其v-t图象如图所示.已知汽车的质量为m=1×103kg,汽车受到地面的阻力为车重的0.1倍,则以下说法正确的是( )| A. | 汽车在前5s内的牵引力为5×103N | |
| B. | 汽车速度为25m/s时的加速度为5m/s2 | |
| C. | 汽车的额定功率为100 kW | |
| D. | 汽车的最大速度为80 m/s |
2.一个从静止开始做匀加速直线运动的物体,从开始运动起,连续通过三段位移的时间分别是1s、2s、3s,则这三段位移的长度之比分别是( )
| A. | 1:22:32 | B. | 1:23:33 | C. | 1:2:3 | D. | 1:3:5 |
 图甲所示为示波管的原理图,图乙表示荧光屏界面,从发热的灯丝射出的电子初速度很小,可视为零,在灯丝和极板P之间所加电压为U1,在两对偏转电极XX′和YY′所加的电压分别为U2和U3,如果U1>0,U2=U3=0,则从电子枪射出的电子束将打在荧光屏的中心O点,如果U3=0,U2的大小随时间变化,其规律如图丙所示,则荧光屏上将出现一条水平亮线.已知U1=2500V,每块偏转极板的长度l都等于4cm,两块正对极板之间的距离d=1cm,设极板之间的电场可看作是均匀的,且极板外无电场,在每个电子通过电场区域的极短时间内,电场可视作恒定的,XX′极板的右端到荧光屏的距离L=8cm,荧光屏界面的直径D=20cm,要使电子都能打在荧光屏上,U2的最大值U是多少伏?
图甲所示为示波管的原理图,图乙表示荧光屏界面,从发热的灯丝射出的电子初速度很小,可视为零,在灯丝和极板P之间所加电压为U1,在两对偏转电极XX′和YY′所加的电压分别为U2和U3,如果U1>0,U2=U3=0,则从电子枪射出的电子束将打在荧光屏的中心O点,如果U3=0,U2的大小随时间变化,其规律如图丙所示,则荧光屏上将出现一条水平亮线.已知U1=2500V,每块偏转极板的长度l都等于4cm,两块正对极板之间的距离d=1cm,设极板之间的电场可看作是均匀的,且极板外无电场,在每个电子通过电场区域的极短时间内,电场可视作恒定的,XX′极板的右端到荧光屏的距离L=8cm,荧光屏界面的直径D=20cm,要使电子都能打在荧光屏上,U2的最大值U是多少伏? 如图,小球A以速率v0=6m/s向右运动时跟静止的小球B发生碰撞,碰后A球以$\frac{v_0}{2}$的速率弹回,而B球以$\frac{v_0}{3}$的速率向右运动.求:
如图,小球A以速率v0=6m/s向右运动时跟静止的小球B发生碰撞,碰后A球以$\frac{v_0}{2}$的速率弹回,而B球以$\frac{v_0}{3}$的速率向右运动.求: 如图,一很长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳两端各系一小球a和b,静置于地面;b球质量是a球质量的2倍,用手托往,高度为h,此时轻绳刚好拉紧.从静止开始释放b后,
如图,一很长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳两端各系一小球a和b,静置于地面;b球质量是a球质量的2倍,用手托往,高度为h,此时轻绳刚好拉紧.从静止开始释放b后, 如图所示,质量为m和M的物块用不可伸长的轻绳连接,且M=4m,M放在倾角为θ=30°的固定光滑斜面上,而m能沿杆在竖直方向滑动,杆和滑轮中心间的距离为$\sqrt{3}$m,求当m由A点静止开始下落1m时的速度多大?(轮、绳质量及各种摩擦均不计,结果保留最简根式,取g=10m/s2)
如图所示,质量为m和M的物块用不可伸长的轻绳连接,且M=4m,M放在倾角为θ=30°的固定光滑斜面上,而m能沿杆在竖直方向滑动,杆和滑轮中心间的距离为$\sqrt{3}$m,求当m由A点静止开始下落1m时的速度多大?(轮、绳质量及各种摩擦均不计,结果保留最简根式,取g=10m/s2)
