题目内容
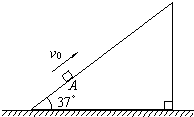如图所示，固定不动的足够长斜面倾角θ=37°，一个物体以v0=12m/s的初速度，从斜面A点处开始自行沿斜面向上运动，加速度大小为a=8.0m/s2．（g=10m/s2，sin 37°=0.6，cos 37°=0.8）求：（1）物体沿斜面上升的最大距离
（2）物体与斜面间动摩擦因数
（3）据条件判断物体上升到最高点后能否返回？若能，求返回时的加速度．
分析：（1）对于上滑过程，根据运动学速度位移关系公式列式求解即可；
（2）受力分析后，根据牛顿第二定律列式求解即可；
（3）下滑过程，根据动能定理求出物体返回到A处时的速度大小v．
（2）受力分析后，根据牛顿第二定律列式求解即可；
（3）下滑过程，根据动能定理求出物体返回到A处时的速度大小v．
解答：解：
（1）上滑过程，由运动学公式v2=2ax得
物体沿斜面上升的最大距离x=
=
m=9m
（2）物体上滑时受力分析如图所示；
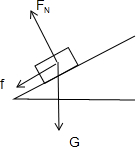
上滑过程，由牛顿第二定律得：mgsinθ+μmgcosθ=ma
解得：μ=0.25
（3）物体沿斜面下滑时受力分析如图所示：
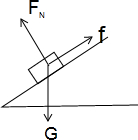
沿斜面方向上：mgsinθ＞μmgcosθ，所以可以下滑
由牛顿第二定律得：mgsinθ-μmgcosθ=ma′
代入数据解得：a′=4 m/s2
答：
（1）物体沿斜面上滑的最大距离x为9m；
（2）物体与斜面间的动摩擦因数μ为0.25；
（3）能，返回时的加速度为4m/s2．
（1）上滑过程，由运动学公式v2=2ax得
物体沿斜面上升的最大距离x=
| v02 |
| 2a |
| 122 |
| 2×8 |
（2）物体上滑时受力分析如图所示；
上滑过程，由牛顿第二定律得：mgsinθ+μmgcosθ=ma
解得：μ=0.25
（3）物体沿斜面下滑时受力分析如图所示：
沿斜面方向上：mgsinθ＞μmgcosθ，所以可以下滑
由牛顿第二定律得：mgsinθ-μmgcosθ=ma′
代入数据解得：a′=4 m/s2
答：
（1）物体沿斜面上滑的最大距离x为9m；
（2）物体与斜面间的动摩擦因数μ为0.25；
（3）能，返回时的加速度为4m/s2．
点评：本题是已知上滑时的运动情况确定受力情况，然后根据受力情况确定下滑时的运动情况，求解出加速度是关键．
练习册系列答案
相关题目
如图所示，固定不动的正点电荷A，带电量为Q=1.0×10-6 C，点电荷B从距A无穷远的电势为零处移到距A为3m、电势为3000V的P点，电场力做功-1.8×10-3 J，求：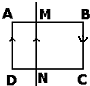
如图所示，固定不动的绝缘直导线MN和可以自由移动的矩形线框ABCD位于同一平面内，MN与AD、BC边平行且离AD边较近，当导线中通以向上的电流，线框中通以顺时针电流时，线框的运动情况是（ ）
（2011?门头沟区一模）如图所示，固定不动的水平平台长L=1.25m，高h=0.80m，货物（可以视为质点）质量m=4.0kg静止在水平平台的左端，商场工作人员用F=24N的水平力把货物施向右拉动一段距离后撤去作用力，货物从平台上又滑动一段距离后落在水平地面上，落地点到平台右端的水平距离s=0.40m．货物与平台之间的动摩擦因数μ=0.20，取重力加速度g=10m/s2．求：