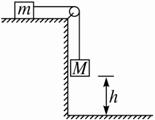
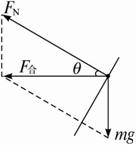
题目内容
如图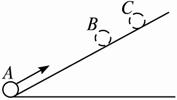
图
解析:由于斜面粗糙,小球克服摩擦力做功,机械能转化为内能,所以小球的机械能不守恒,可应用动能定理和功能原理求解.
小球在由A点到B点的过程中,动能的损失量对应于克服合外力所做的功,机械能的损失量对应于克服摩擦力所做的功.由动能定理得:WG+WF=ΔEk=-50 J
由功能原理得:WF=ΔE=-10 J
又F∶G=WF∶WG
由以上三式可得: F∶G=1∶4
小球在由B点到C点的过程中,动能减少10 J,由动能定理得:
WG′+WF′=ΔEk′=-10 J,
又WF′∶WG′=F∶G=1∶4,
由以上两式可得:WF′=-2 J.
所以,上升过程中(从A到C)小球克服摩擦力做功12 J,一上一下,全过程小球克服摩擦力做功24 J.在小球运动的全过程中由动能定理得:WF总=Ekt-Ek0,解得小球运动至出发点A时的动能为:Ekt=WF总+Ek0=-24 J+60 J=36 J.
答案:36 J

练习册系列答案
相关题目
如图5-10-4 所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止,人与雪橇的总质量为70 kg .表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题.
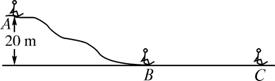
图
位置 | A | B | C |
速度(m/s) | 2.0 | 12.0 | 0 |
时刻(s) | 0 | 4 | 10 |
(1)人与雪橇从A到B的过程中,损失的机械能为多少?
(2)设人与雪橇在BC段所受阻力恒定,求阻力大小.(g取