题目内容
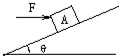如图，质量m=2.5kg的物体A，在水平推力F的作用下，恰能沿倾角为θ=37°的斜面匀速上滑，g取10m/s2．（1）若A与斜面间动摩擦数为μ=0.5，求F．（sin37°=0.6，cos37°=0.8）
（2）若斜面是光滑的，推力F=15N，方向为平行斜面向上，为使A在斜面上运动的加速度大小小于1m/s2，求倾角的正弦值sinθ的范围．
分析：对物体受力分析，根据平衡条件列方程求解；
加速度大小小于1m/s2，包括加速度的方向可能向上和向下两种情况，对物体受力分析，根据牛顿第二定律列方程求解．
加速度大小小于1m/s2，包括加速度的方向可能向上和向下两种情况，对物体受力分析，根据牛顿第二定律列方程求解．
解答：解：（1）对物体受力分析，根据平衡条件：
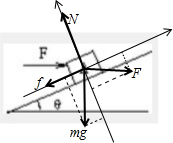
沿斜面方向，Fcos37°-f-mgsin37°=0
垂直斜面方向，mgcos37°+Fsin37°=N
又f=μN
联立三个方程得：F=50N；
（2）若加速度方向沿斜面向上，根据牛顿第二定律：F-mgsinθ=ma
15-25sinθ=2.5×1，得：sinθ=0.5；
若加速度方向沿斜面向下，根据牛顿第二定律：mgsinθ-F=ma
带入数据得：sinθ=0.7
故sinθ的范围是0.5＜sinθ＜0.7；
答：（1）若A与斜面间动摩擦数为μ=0.5，F为50N；
（2）若斜面是光滑的，推力F=15N，方向为平行斜面向上，为使A在斜面上运动的加速度大小小于1m/s2，倾角的正弦值sinθ的范围为：0.5＜sinθ＜0.7．
沿斜面方向，Fcos37°-f-mgsin37°=0
垂直斜面方向，mgcos37°+Fsin37°=N
又f=μN
联立三个方程得：F=50N；
（2）若加速度方向沿斜面向上，根据牛顿第二定律：F-mgsinθ=ma
15-25sinθ=2.5×1，得：sinθ=0.5；
若加速度方向沿斜面向下，根据牛顿第二定律：mgsinθ-F=ma
带入数据得：sinθ=0.7
故sinθ的范围是0.5＜sinθ＜0.7；
答：（1）若A与斜面间动摩擦数为μ=0.5，F为50N；
（2）若斜面是光滑的，推力F=15N，方向为平行斜面向上，为使A在斜面上运动的加速度大小小于1m/s2，倾角的正弦值sinθ的范围为：0.5＜sinθ＜0.7．
点评：本题考查牛顿第二定律的应用，要正确分析物体的受力情况，运用正交分解法处理多力平衡问题．
练习册系列答案
名校课堂系列答案
相关题目
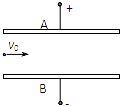如图，质量m=5×10-8kg的带负电微粒以v0=2m/s的速度从水平放置的金属板A、B的中央飞入板间，已知板长L=10cm，板间距离d=2cm．当U0=1000V时，带电粒子恰好沿线穿过板间，取g=10m/s2，求：
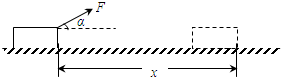如图，质量m=4.0kg的物体在恒力F=40N作用下，由静止开始沿水平面运动x=2.0m，力F与水方向的夹角α=37°，物体与水平面间的动摩擦因数μ=0.5，求该过程中：
