题目内容
5.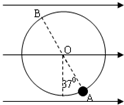 水平向右的匀强电场中,用长为R的轻质细线在O点悬挂一质量为m的带电小球,静止在A处,AO的连线与竖直方向夹角为37°
水平向右的匀强电场中,用长为R的轻质细线在O点悬挂一质量为m的带电小球,静止在A处,AO的连线与竖直方向夹角为37°(1)小球的电性及绳子对它的拉力的大小
(2)现给小球施加一个沿圆弧切线方向的初速度V0,小球便在竖直面内运动,为使小球能在竖直面内完成圆周运动,这个初速度V0至少应为多大?
分析 (1)根据受力分析,依据平衡条件,分析电场力的方向,从而确定小球的电性.并求绳子的拉力大小.
(2)将电场力与重力合成等效成重力加速度,由牛顿第二定律求最小速度,并根据运动定理,即可求解.
解答 解:(1)静止时,小球所受的电场力水平向右,所以小球带正电.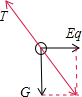
静止时对球受力分析如右图,则有
绳子拉力 T=$\frac{mg}{cos37°}$=$\frac{5}{4}$mg
(2)小球所受的电场力 qE=mgtan37°=$\frac{3}{4}$mg
将电场力与重力合成,“等效”场力为 G′=$\sqrt{(mg)^{2}+(qE)^{2}}$=$\frac{5}{4}$mg,与T反向
“等效”场重力加速度 g′=$\frac{5}{4}$g
与重力场相类比可知,小球能在竖直平面内完成圆周运动的速度速度位置在AO连线B处,且最小速度为 vB=$\sqrt{g′R}$
从B到A运用动能定理,可得 G′•2R=$\frac{1}{2}m{v}_{0}^{2}$-$\frac{1}{2}m{v}_{B}^{2}$
即$\frac{5}{4}$mg•2R=$\frac{1}{2}m{v}_{0}^{2}$-$\frac{1}{2}m•\frac{5}{4}gR$
解得v0=$\frac{5}{2}\sqrt{gR}$
答:
(1)小球带正电,绳子对它的拉力的大小为$\frac{5}{4}$mg.
(2)为使小球能在竖直面内完成圆周运动,这个初速度V0至少应为$\frac{5}{2}\sqrt{gR}$.
点评 此题要掌握平衡条件,寻找电场力与重力的关系.并等效成新的重力加速度,同时掌握动能定理,注意功的正负值.

练习册系列答案
相关题目
15.用手握瓶子,瓶子静止在手中,如图所示,瓶始终处于竖直方向,则下列说法正确的是( )
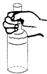

| A. | 手对瓶子的压力等于瓶子所受的重力 | |
| B. | 手对瓶子的摩擦力等于瓶子所受的重力 | |
| C. | 手握得越紧,手对瓶子的摩擦力越大 | |
| D. | 手对瓶子的摩擦力必须大于瓶子所受的重力 |
16.静止在粗糙水平地面上的水箱,受到一个逐渐增大的水平推力F作用,而木箱仍静止不动,则在这个过程中,说法正确的是( )
| A. | 木箱与地面间的摩擦力始终大于F | |
| B. | 木箱所受合力始终为零 | |
| C. | 木箱与地面间的摩擦力随F增大而增大 | |
| D. | 木箱所受的合力逐渐增大 |
13.下列说法中正确的是( )
| A. | 一定质量的理想气体,其分子势能可以改变 | |
| B. | 悬浮在液体中的固体微粒越小,布朗运动就越明显 | |
| C. | 封闭在体积不变的容器中的气体,温度升高气体分子对器壁单位面积上的平均作用力增大 | |
| D. | 用打气筒的活塞压缩气体很费力,说明分子间有斥力 | |
| E. | 物体的温度越高,分子热运动越剧烈,分子平均动能就越大 |
20.光滑绝缘水平面上,B、C、D四等分线段AE,M、N是两个完全一样的小球,带有等量同种电荷,C处固定一竖直绝缘挡板,若小球N放在D处,将小球M放在C处,同时由静止释放两球,小球N到达E处的速度大小为v;若移去挡板,小球N仍放在D处,而将小球M放在B处,同时由静止释放两球,小球N到达E处的速度大小为v′,则v′与v大小之比是( )
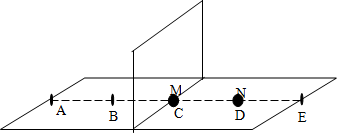

| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
10.某物体的v-t图线如图所示,则该物体 ( )
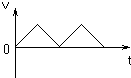

| A. | 做往复运动 | B. | 位移一直在增大 | ||
| C. | 朝某一方向做直线运动 | D. | 以上说法都不正确 |
17.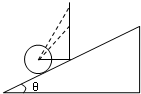 如图所示,小球用细绳系住始终静止在倾角为θ的光滑斜面上,当细绳方向由水平逐渐向上偏移时,绳的拉力F和斜面对小球的支持力FN将( )
如图所示,小球用细绳系住始终静止在倾角为θ的光滑斜面上,当细绳方向由水平逐渐向上偏移时,绳的拉力F和斜面对小球的支持力FN将( )
 如图所示,小球用细绳系住始终静止在倾角为θ的光滑斜面上,当细绳方向由水平逐渐向上偏移时,绳的拉力F和斜面对小球的支持力FN将( )
如图所示,小球用细绳系住始终静止在倾角为θ的光滑斜面上,当细绳方向由水平逐渐向上偏移时,绳的拉力F和斜面对小球的支持力FN将( )| A. | F逐渐增大,FN逐渐减小 | B. | F先增大后减小,FN逐渐减小 | ||
| C. | F逐渐减小,FN逐渐增大 | D. | F先减小后增大,FN逐渐减小 |
4.如图所示,A、B是两个摩擦传动轮,两轮半径大小关系为RA=2RB,则两轮边缘上的( )


| A. | 角速度之比ωA:ωB=1:2 | B. | 周期之比TA:TB=1:2 | ||
| C. | 转速之比nA:nB=1:2 | D. | 向心加速度之比aA:aB=2:1 |