题目内容
 如图,光滑固定斜面倾角为α,斜面底端固定有垂直斜面的挡板C,斜面顶端固定有光滑定滑轮.质量为m的物体A经一轻质弹簧与下方挡板上的质量也为m的物体B相连,弹簧的劲度系数为k,A、B都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩.开始时各段绳都处于伸直状态,A上方的一段绳平行于斜面.现在挂钩上挂一质量为M的物体D并从静止状态释放,已知它恰好能使B离开挡板但不继续上升.若让D带上正电荷q,同时在D运动的空间中加上方向竖直向下的匀强电场,电场强度的大小为E,仍从上述初始位置由静止状态释放D,则这次B刚离开挡板时D的速度大小是多少?已知重力加速度为g.
如图,光滑固定斜面倾角为α,斜面底端固定有垂直斜面的挡板C,斜面顶端固定有光滑定滑轮.质量为m的物体A经一轻质弹簧与下方挡板上的质量也为m的物体B相连,弹簧的劲度系数为k,A、B都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩.开始时各段绳都处于伸直状态,A上方的一段绳平行于斜面.现在挂钩上挂一质量为M的物体D并从静止状态释放,已知它恰好能使B离开挡板但不继续上升.若让D带上正电荷q,同时在D运动的空间中加上方向竖直向下的匀强电场,电场强度的大小为E,仍从上述初始位置由静止状态释放D,则这次B刚离开挡板时D的速度大小是多少?已知重力加速度为g.分析:应用平衡条件求出弹簧形变量,应用机械能守恒定律可以求出D的速度.
解答:解:挂钩没有挂D时,A压缩弹簧,弹簧的压缩量为x1,
对A有:mgsinα=kx1,则有:x1=
,
挂钩挂上D后,B刚好离开挡板时弹簧的伸长量为x2,
对B有:mgsinα=kx2,则有:x2=
,
该过程A沿斜面上升的距离和D下降的高度都是x1+x2,且A、D的初速度、末速度都为零.
设该过程弹性势能的增量为△E,由系统机械能守恒有:
mg(x1+x2)sinα-Mg(x1+x2)+△E=0;
将D带电后,D在电场中运动,电场力对D作正功,设B刚离开挡板时D的速度为υ,D下降x1+x2过程系统能量守恒,有:mg(x1+x2)sinα-Mg(x1+x2)+△E-qE(x1+x1)+
(m+M)υ2=0;
由以上四个方程消去△E,得:υ=2
.
答:B刚离开挡板时D的速度大小是2
.
对A有:mgsinα=kx1,则有:x1=
| mgsinα |
| k |
挂钩挂上D后,B刚好离开挡板时弹簧的伸长量为x2,
对B有:mgsinα=kx2,则有:x2=
| mgsinα |
| k |
该过程A沿斜面上升的距离和D下降的高度都是x1+x2,且A、D的初速度、末速度都为零.
设该过程弹性势能的增量为△E,由系统机械能守恒有:
mg(x1+x2)sinα-Mg(x1+x2)+△E=0;
将D带电后,D在电场中运动,电场力对D作正功,设B刚离开挡板时D的速度为υ,D下降x1+x2过程系统能量守恒,有:mg(x1+x2)sinα-Mg(x1+x2)+△E-qE(x1+x1)+
| 1 |
| 2 |
由以上四个方程消去△E,得:υ=2
|
答:B刚离开挡板时D的速度大小是2
|
点评:分析清楚物体运动过程,应用平衡条件、胡克定律、机械能守恒定律即可正确解题.

练习册系列答案
相关题目
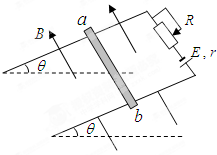
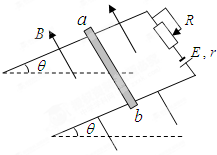 如图所示,在倾θ=30°的绝缘斜面上,固定一L=0.25m的平行金属导轨,在导轨上端接入电源和滑动变阻器,电源电动E=12V,内r=1Ω,一质m=20g的金属ab与两导轨垂直并接触良好,整个装置处于磁感应强B=0.8T,方向垂直于斜面向上的匀强磁场中.金属导轨光滑,导轨与金属棒的电阻不计,g=10m/s2,要保持金属棒在导轨上静止,求:
如图所示,在倾θ=30°的绝缘斜面上,固定一L=0.25m的平行金属导轨,在导轨上端接入电源和滑动变阻器,电源电动E=12V,内r=1Ω,一质m=20g的金属ab与两导轨垂直并接触良好,整个装置处于磁感应强B=0.8T,方向垂直于斜面向上的匀强磁场中.金属导轨光滑,导轨与金属棒的电阻不计,g=10m/s2,要保持金属棒在导轨上静止,求: