题目内容
13.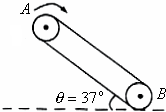 传送带与水平面夹角37°,皮带以12m/s的速率运动,皮带轮沿顺时针方向转动,如图所示.今在传送带上端A处无初速地放上一个质量为m=0.5kg的小物块,它与传送带间的动摩擦因数为0.75,若传送带A到B的长度为24m,g取10m/s2,则物体从A运动到B的时间为多少?
传送带与水平面夹角37°,皮带以12m/s的速率运动,皮带轮沿顺时针方向转动,如图所示.今在传送带上端A处无初速地放上一个质量为m=0.5kg的小物块,它与传送带间的动摩擦因数为0.75,若传送带A到B的长度为24m,g取10m/s2,则物体从A运动到B的时间为多少?
分析 物体放在传送带上后,开始阶段,传送带的速度大于物体的速度,传送带给物体一沿斜面向下的滑动摩擦力,物体由静止开始加速下滑,当物体加速至与传送带速度相等时,由于μ=tanθ,物体相对于传送带静止,做匀速运动,根据牛顿第二定律和运动学公式结合求解时间.
解答 解:开始阶段,由牛顿第二定律得:
mgsinθ+μmgcosθ=ma1
得:a1=gsinθ+μgcosθ=12m/s2
物体加速至与传送带速度相等时需要的时间为:
t1=$\frac{v}{{a}_{1}}$=$\frac{12}{12}$=1s,
通过的位移为:x1=$\frac{1}{2}{a}_{1}{t}_{1}^{2}$=$\frac{1}{2}×12×1$=6m
由题:μ=tanθ,物体相对于传送带静止,物体接着做匀速运动,运动时间为:
t2=$\frac{L-{x}_{1}}{v}$=$\frac{24-6}{12}$=1.5s
故小物块从A运动到B的时间为:
t=t1+t2=2.5s.
答:物体从A运动到B的时间为2.5s
点评 从上述例题可以总结出,皮带传送物体所受摩擦力可能发生突变,不论是其大小的突变,还是其方向的突变,都发生在物体的速度与传送带速度相等的时刻.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
19. 如图所示,一个上表面光滑的斜面体M置于水平地面上,它的两个斜面与水平面间的夹角分别为α、β,且α<β,M的顶端装有一定滑轮,一轻质细绳跨过定滑轮后连接A、B两个小物块,细绳与各自的斜面平行,不计绳与滑轮间的摩擦,A、B恰好在同一高度处于静止状态,剪断细绳后,A、B滑至斜面底端,M始终保持静止,则( )
如图所示,一个上表面光滑的斜面体M置于水平地面上,它的两个斜面与水平面间的夹角分别为α、β,且α<β,M的顶端装有一定滑轮,一轻质细绳跨过定滑轮后连接A、B两个小物块,细绳与各自的斜面平行,不计绳与滑轮间的摩擦,A、B恰好在同一高度处于静止状态,剪断细绳后,A、B滑至斜面底端,M始终保持静止,则( )
 如图所示,一个上表面光滑的斜面体M置于水平地面上,它的两个斜面与水平面间的夹角分别为α、β,且α<β,M的顶端装有一定滑轮,一轻质细绳跨过定滑轮后连接A、B两个小物块,细绳与各自的斜面平行,不计绳与滑轮间的摩擦,A、B恰好在同一高度处于静止状态,剪断细绳后,A、B滑至斜面底端,M始终保持静止,则( )
如图所示,一个上表面光滑的斜面体M置于水平地面上,它的两个斜面与水平面间的夹角分别为α、β,且α<β,M的顶端装有一定滑轮,一轻质细绳跨过定滑轮后连接A、B两个小物块,细绳与各自的斜面平行,不计绳与滑轮间的摩擦,A、B恰好在同一高度处于静止状态,剪断细绳后,A、B滑至斜面底端,M始终保持静止,则( )| A. | 物块A的质量大于B的质量 | |
| B. | 物块A对斜面体M的压力大于B对斜面体M的压力 | |
| C. | 两物块达到斜面底端时,物块A重力的瞬时功率较大 | |
| D. | 在滑块A、B下滑的过程中,斜面体受到水平向左的摩擦力 |
1.利用如图1所示的装置测量滑块与水平长木板之间的动摩擦因数μ,一滑块放在水平长木扳上,左侧拴有一细软线,跨过固定在长木板边缘的定滑轮与一重物相连,在重物的牵引下,滑块在长木板上向左运动,重物落地后,滑块继续向左做匀减速运动,在长木板上安装有两个光电门,其中光电门甲固定在长木板的右侧,光电门乙的位置可移动,当一带有挡光片的滑块从右端向左端滑动时,与两个光电门都相连的计时器可以显示出挡光片从光电门甲至乙所用的时间t,每次都使滑块从同一点由静止开始运动,且滑块开始的位置到光电门甲之间的距离与重物开始的位置到地面的距离相等均为L,改变光电门乙到光电门甲之间的距离X,进行多次测量,并用米尺测量出光电门甲、乙之间相应的距离X,记下相应的t值,所得数据如表所示.

请你根据题目所给数据完成下列问题(g=9.8m/s2,结果保留两位有效数字):
(1)根据表中所给的数据,在图2的坐标纸上画出$\frac{X}{t}$-t图线;
(2)根据所画出的$\frac{X}{t}$-t图线,得出滑块加速度的大小为a=3.0m/s2;
(3)滑块与水平长木板之间的动摩擦因数μ=0.31.
| X(m) | 0.200 | 0.400 | 0.600 | 0.700 | 0.800 | 0.900 | 0.950 |
| t(s) | 0.088 | 0.189 | 0.311 | 0.385 | 0.473 | 0.600 | 0.720 |
| $\frac{X}{t}$(m/s) | 2.27 | 2.12 | 1.93 | 1.82 | 1.69 | 1.50 | 1.32 |

请你根据题目所给数据完成下列问题(g=9.8m/s2,结果保留两位有效数字):
(1)根据表中所给的数据,在图2的坐标纸上画出$\frac{X}{t}$-t图线;
(2)根据所画出的$\frac{X}{t}$-t图线,得出滑块加速度的大小为a=3.0m/s2;
(3)滑块与水平长木板之间的动摩擦因数μ=0.31.
8.甲乙丙三辆汽车以相同速度同时通过某一路标,从此时开始甲车一直做匀速直线运动,乙车先加速后减速,丙车先减速后加速,它们经过下一个路标时的速度又相同,则最先通过下一路标的应是( )
| A. | 甲 | B. | 乙 | ||
| C. | 丙 | D. | 条件不足,无法判断 |
2.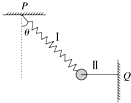 如图所示,质量为m的小球与弹簧Ⅰ和水平细绳Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q两点.球静止时,Ⅰ中拉力大小为T1,Ⅱ中拉力大小为T2,当仅剪断Ⅰ、Ⅱ其中一根的瞬间,球的加速度a应是( )
如图所示,质量为m的小球与弹簧Ⅰ和水平细绳Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q两点.球静止时,Ⅰ中拉力大小为T1,Ⅱ中拉力大小为T2,当仅剪断Ⅰ、Ⅱ其中一根的瞬间,球的加速度a应是( )
 如图所示,质量为m的小球与弹簧Ⅰ和水平细绳Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q两点.球静止时,Ⅰ中拉力大小为T1,Ⅱ中拉力大小为T2,当仅剪断Ⅰ、Ⅱ其中一根的瞬间,球的加速度a应是( )
如图所示,质量为m的小球与弹簧Ⅰ和水平细绳Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q两点.球静止时,Ⅰ中拉力大小为T1,Ⅱ中拉力大小为T2,当仅剪断Ⅰ、Ⅱ其中一根的瞬间,球的加速度a应是( )| A. | 若剪断Ⅰ,则a=g,方向竖直向下 | |
| B. | 若剪断Ⅱ,则a=$\frac{{T}_{2}}{m}$,方向水平向左 | |
| C. | 若剪断Ⅰ,则a=$\frac{{T}_{1}}{m}$,方向沿Ⅰ的延长线方向 | |
| D. | 若剪断Ⅱ,则a=g,方向竖直向上 |
3.下列物理量属于矢量的是( )
| A. | 电场强度 | B. | 长度 | C. | 质量 | D. | 时间 |
 如图所示,水平放置的弹簧左端固定,小物块P(可视为质点)置于水平桌面上的A点,并与弹簧右端接触,此时弹簧处于原长.现用水平向左的推力将P缓慢地推至B点,此时弹簧的弹性势能为EP=21J.撤去推力后,P沿桌面滑上一个停在光滑水平地面上的长木板Q上,已知P、Q的质量分别为m=2kg、M=4kg,A、B间的距离Ll=4m,A距桌子边缘C的距离L2=2m,P与桌面及P与Q间的动摩擦因数都为μ=0.1,g取10m/s2,求:
如图所示,水平放置的弹簧左端固定,小物块P(可视为质点)置于水平桌面上的A点,并与弹簧右端接触,此时弹簧处于原长.现用水平向左的推力将P缓慢地推至B点,此时弹簧的弹性势能为EP=21J.撤去推力后,P沿桌面滑上一个停在光滑水平地面上的长木板Q上,已知P、Q的质量分别为m=2kg、M=4kg,A、B间的距离Ll=4m,A距桌子边缘C的距离L2=2m,P与桌面及P与Q间的动摩擦因数都为μ=0.1,g取10m/s2,求:
 如图所示,人重300N,物体重200N,地面粗糙,当人用100N的力向下拉绳子时,人和物体均处于静止状态,求:
如图所示,人重300N,物体重200N,地面粗糙,当人用100N的力向下拉绳子时,人和物体均处于静止状态,求: