题目内容
17. 在水平面上,用与水平方向成θ=37°角斜向上方的拉力F=20N拉着一个质量m=2kg的物体从静止开始运动,物体与水平面间的动摩擦因数为μ=0.25,物体运动t=2s时撤去拉力.取g=10m/s2.求:
在水平面上,用与水平方向成θ=37°角斜向上方的拉力F=20N拉着一个质量m=2kg的物体从静止开始运动,物体与水平面间的动摩擦因数为μ=0.25,物体运动t=2s时撤去拉力.取g=10m/s2.求:(1)物体做匀加速直线运动的加速度是多少?
(2)撤去拉力后物块在水平面上还能向前滑行的距离是多少?
分析 (1)根据牛顿第二定律求出匀加速运动的加速度.
(2)根据速度时间公式求出2s末的速度,根据牛顿第二定律求出撤去拉力后的加速度,结合速度位移公式求出继续向前滑行的距离.
解答 解:(1)由牛顿第二定律得:
Fcosθ-μ(mg-Fsinθ)=ma
解得加速度为:a=$\frac{Fcosθ-μ(mg-Fsinθ)}{m}$=$\frac{20×0.8-0.25×(20-20×0.6)}{2}=7m/{s}^{2}$
(2)2s末的速度为:v=at=7×2m/s=14m/s,
撤去F后的加速度为:$a′=\frac{μmg}{m}=μg=2.5m/{s}^{2}$,
则继续向前滑行的距离为:x′=$\frac{{v}^{2}}{2a′}=\frac{1{4}^{2}}{2×2.5}=39.2$m.
答:(1)物体做匀加速直线运动的加速度为7m/s2;
(2)撤去拉力后物块在水平面上还能向前滑行的距离是39.2m.
点评 本题考查了牛顿第二定律和运动学公式的综合,知道加速度是联系力学和运动学的桥梁,注意在撤去拉力前后物体所受的摩擦力不同.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
7. 如图所示是一定质量理想气体的p-T图线(p为气体压强,T为热力学温度),气体状态从图中A沿直线变化到B的过程中,下列表述正确的是( )
如图所示是一定质量理想气体的p-T图线(p为气体压强,T为热力学温度),气体状态从图中A沿直线变化到B的过程中,下列表述正确的是( )
 如图所示是一定质量理想气体的p-T图线(p为气体压强,T为热力学温度),气体状态从图中A沿直线变化到B的过程中,下列表述正确的是( )
如图所示是一定质量理想气体的p-T图线(p为气体压强,T为热力学温度),气体状态从图中A沿直线变化到B的过程中,下列表述正确的是( )| A. | 气体的体积逐渐变小 | |
| B. | 外界对气体做功使气体内能增加 | |
| C. | 每个气体分子热运动的动能都逐渐增大 | |
| D. | 气体从外界吸收的热量大于气体内能的增加量 |
8.14C发生放射性衰变成为14N,半衰期约5700年.已知植物存活期间,其体内14C与12C的比例不变;生命活动结束后,14C的比例持续减小.现通过测量得知,某古木样品中14C的比例正好是现代植物所制样品的二分之一.下列说法正确的是( )
| A. | 该古木的年代距今约5700年 | |
| B. | 12C、13C、14C具有相同的中子数 | |
| C. | 14C衰变为14N的过程中放出β射线 | |
| D. | 增加样品测量环境的压强将加速14C的衰变 |
2.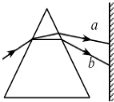 如图,一束光经玻璃三棱镜折射后分为两束单色光a、b,波长分别为λa、λb,该玻璃对单色光a、b的折射率分别为na、nb,则( )
如图,一束光经玻璃三棱镜折射后分为两束单色光a、b,波长分别为λa、λb,该玻璃对单色光a、b的折射率分别为na、nb,则( )
 如图,一束光经玻璃三棱镜折射后分为两束单色光a、b,波长分别为λa、λb,该玻璃对单色光a、b的折射率分别为na、nb,则( )
如图,一束光经玻璃三棱镜折射后分为两束单色光a、b,波长分别为λa、λb,该玻璃对单色光a、b的折射率分别为na、nb,则( )| A. | λa<λb,na>nb | B. | λa>λb,na<nb | C. | λa<λb,na<nb | D. | λa>λb,na>nb |
6.物体在一对平衡力作用下运动( )
| A. | 其机械能一定保持不变 | B. | 其动能一定保持不变 | ||
| C. | 其重力势能一定保持不变 | D. | 其重力势能、动能一定都保持不变 |
7.如图是甲、乙两物体做直线运动的v-t图象.下列表述正确的是( )


| A. | 0~1s内甲和乙的位移相等 | B. | 乙做匀加速直线运动 | ||
| C. | 甲和乙的加速度方向相同 | D. | 甲和乙的速度方向相同 |
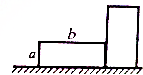 如图所示,质量为$\frac{m}{2}$的均匀长方体木块,边长分别是a和b,平卧在水平地面上,现把它竖起来,人至少要对它做功为$\frac{mgb}{4}$.
如图所示,质量为$\frac{m}{2}$的均匀长方体木块,边长分别是a和b,平卧在水平地面上,现把它竖起来,人至少要对它做功为$\frac{mgb}{4}$. 一摩托车由静止开始在平直的公路上行驶,其运动过程的v-t图象如图所示.求:
一摩托车由静止开始在平直的公路上行驶,其运动过程的v-t图象如图所示.求: