题目内容
 如图轻质弹簧长为L,竖直固定在地面上,质量为m的小球,离地面高度为H处,由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x,在下落过程中小球受到的空气阻力恒为f,则弹簧在压缩到最短时具有的弹性势能为( )
如图轻质弹簧长为L,竖直固定在地面上,质量为m的小球,离地面高度为H处,由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x,在下落过程中小球受到的空气阻力恒为f,则弹簧在压缩到最短时具有的弹性势能为( )A.(mg-f)(H-L+x)
B.mg(H-L+x)-f(H-L)
C.mgH-f(H-L)
D.mg(L-x)+f(H-L+x)
【答案】分析:小球从开始下落到弹簧压缩到最短的过程中,小球的重力势能转化为弹簧的弹性势能、内能,由能量守恒定律求解弹簧的弹性势能.
解答:解:小球从开始下落到弹簧压缩到最短的过程中,小球的重力势能转化为弹簧的弹性势能、内能,根据能量守恒定得:mg[H-(L-x)]=f(H-L+x)+EP,得:弹簧在压缩到最短时具有的弹性势能为EP=mg(H-L+x)-f(H-L+x)=(mg-f)(H-L+x).
故选A
点评:运用能量守恒定律分析问题时,首先搞清涉及几种形式的能,其次分清什么能在增加,什么能在减小,再根据能量的变化量列方程.
解答:解:小球从开始下落到弹簧压缩到最短的过程中,小球的重力势能转化为弹簧的弹性势能、内能,根据能量守恒定得:mg[H-(L-x)]=f(H-L+x)+EP,得:弹簧在压缩到最短时具有的弹性势能为EP=mg(H-L+x)-f(H-L+x)=(mg-f)(H-L+x).
故选A
点评:运用能量守恒定律分析问题时,首先搞清涉及几种形式的能,其次分清什么能在增加,什么能在减小,再根据能量的变化量列方程.

练习册系列答案
相关题目
 如图轻质弹簧长为L,竖直固定在地面上,质量为m的小球,离地面高度为H处,由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x,在下落过程中小球受到的空气阻力恒为f,则弹簧在压缩到最短时具有的弹性势能为( )
如图轻质弹簧长为L,竖直固定在地面上,质量为m的小球,离地面高度为H处,由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x,在下落过程中小球受到的空气阻力恒为f,则弹簧在压缩到最短时具有的弹性势能为( )
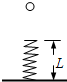
 如图轻质弹簧长为L,竖直固定在地面上,质量为m的小球,离地面高度为H处,由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x,在下落过程中小球受到的空气阻力恒为f,则弹簧在压缩到最短时具有的弹性势能为( )
如图轻质弹簧长为L,竖直固定在地面上,质量为m的小球,离地面高度为H处,由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x,在下落过程中小球受到的空气阻力恒为f,则弹簧在压缩到最短时具有的弹性势能为( )