题目内容
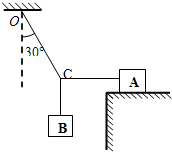
物体A重400N,A与桌面间的最大静摩擦力为120N,AC绳水平,OC绳与竖直方向的夹角为30°,求:
(1)当物体B重100N时,A所受的摩擦力为多少?
(2)如OC绳能够承受的最大拉力为300N,A静止不动,问所挂物体B的最大重量为多少?
分析:先以结点C为研究对象,受到三个细绳的拉力.CB绳的拉力等于物体的重力,根据平衡条件求出CA绳的拉力.再对物体A研究求出A受到的静摩擦力.当A与水平桌面间的最大静摩擦力是120N,此时CA绳的拉力达到120N,判断出OC与CA哪个先达到临界情况,再由平衡条件求出B物体重力的最大值.
解答:解:(1)以结点C为研究对象,建立直角坐标系
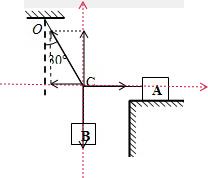
x轴上:T
A=Tsin30°①
y轴上:T
B=G
B=Tcos30° ②
①②联立,得T
A=G
Btan30°
代入其值得T
A=
N;
以A为研究对象,受力分析,可得A受到的静摩擦力f=T
A′=T
A=
N,方向水平向右.
(2)逐渐加大B的重力时,要使系统处于平衡状态,CA绳拉力不能超过A的最大静摩擦力,OC绳能够承受的最大拉力为300N,由上面分析知T
A=Tsin30°,即T:T
A=2:1,故CA先达到最大拉力,由上述表达式可知:
G
B=
=
=120
N;
答:(1)当物体B重100N时,A所受的摩擦力为
N,方向水平向右.
(2)如OC绳能够承受的最大拉力为300N,A静止不动,所挂物体B的最大重量是120
N.
点评:本题是物体平衡问题,其基本思路是:首先确定研究对象,再分析物体的受力情况,最后根据平衡条件列方程求解.
练习册系列答案
相关题目
 物体A重400N,A与桌面间的最大静摩擦力为120N,AC绳水平,OC绳与竖直方向的夹角为30°,求:
物体A重400N,A与桌面间的最大静摩擦力为120N,AC绳水平,OC绳与竖直方向的夹角为30°,求:


 如图所示,绳OC与竖直方向30°角,O为质量不计的光滑的滑轮,用一根绳连接物体A和B,已知物体B重1000N,物体A重400N,物块A空中静止,物体B在地面上静止.求:
如图所示,绳OC与竖直方向30°角,O为质量不计的光滑的滑轮,用一根绳连接物体A和B,已知物体B重1000N,物体A重400N,物块A空中静止,物体B在地面上静止.求: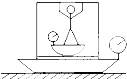 重400N的大木箱放在大磅秤上,箱内的小磅秤上站着一个质量为60kg的人,如图(人与其它物体均处于静止状态),当人用力向上推木箱的顶板时,两磅秤的示数将( )
重400N的大木箱放在大磅秤上,箱内的小磅秤上站着一个质量为60kg的人,如图(人与其它物体均处于静止状态),当人用力向上推木箱的顶板时,两磅秤的示数将( )
