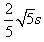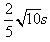题目内容
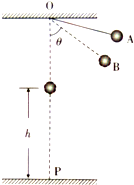 如图所示,质量m=lkg的小球用细线悬挂于0点,线长=0.5m,细线所受拉力达到 F=20N时就会被拉断,将小球从位置A释放,小球运动到细线与竖直方向成θ=53°的B点时速度大小为lm/s,小球运动到0点的正下方时,细线恰好被拉断.若此时小球距水平地面的高度 h=5m,取重力加速度g=10m/s2,求:
如图所示,质量m=lkg的小球用细线悬挂于0点,线长=0.5m,细线所受拉力达到 F=20N时就会被拉断,将小球从位置A释放,小球运动到细线与竖直方向成θ=53°的B点时速度大小为lm/s,小球运动到0点的正下方时,细线恰好被拉断.若此时小球距水平地面的高度 h=5m,取重力加速度g=10m/s2,求:(1)小球摆到B点时,细线对小球的拉力大小;(sin53°=0.8; cos53°=0.6)
(2)求小球落地处到地面上P点的距离.(P点在悬点的正下方)
(说明:以上为原题,从题中可看出B点速度这个条年是多于的)
分析:(1)小球摆到B点时,根据重力沿细线方向的分力与细线拉力的合力提供向心力,列式求解细线对小球的拉力大小;
(2)小球摆到最低点时,由重力和细线的拉力的合力提供向心力,列式求出小球到最低点时的速度.细线被拉断后,小球做平抛运动,由高度h求出平抛运动的时间,再求解小球落地处到地面上P点的距离.
(2)小球摆到最低点时,由重力和细线的拉力的合力提供向心力,列式求出小球到最低点时的速度.细线被拉断后,小球做平抛运动,由高度h求出平抛运动的时间,再求解小球落地处到地面上P点的距离.
解答:解:(1)小球在B点法线方向受到的合外力提供向心力,则根据牛顿第二定律得:
m
=T-mgcos53°…①
解得:T=mgcos53°+m
=10×0.6+1×
=8N… ②
(2)小球摆到最低点时,由重力和细线的拉力的合力提供向心力,则有:
F-mg=m
…③
代入得:20-10=1×
解得:vC=
m/s
绳子断后,小球做平抛运动,竖直方向满足:h=
gt2… ④
水平方向位移大小:x=vCt=vC
=
×
m=
m
答:(1)小球摆到B点时,细线对小球的拉力大小为8N.
(2)小球落地处到地面上P点的距离为
m.
m
| ||
| l |
解得:T=mgcos53°+m
| ||
| L |
| 12 |
| 0.5 |
(2)小球摆到最低点时,由重力和细线的拉力的合力提供向心力,则有:
F-mg=m
| ||
| l |
代入得:20-10=1×
| ||
| 0.5 |
解得:vC=
| 5 |
绳子断后,小球做平抛运动,竖直方向满足:h=
| 1 |
| 2 |
水平方向位移大小:x=vCt=vC
|
| 5 |
|
| 5 |
答:(1)小球摆到B点时,细线对小球的拉力大小为8N.
(2)小球落地处到地面上P点的距离为
| 5 |
点评:本题是向心力知识、牛顿第二定律和平抛运动知识的综合,比较简单.

练习册系列答案
相关题目
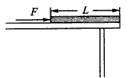
 如图所示,质量m=l kg的物块,以速度v0=4m/s滑上正沿逆时针转动的水平传送带,传送带上A、B两点间的距离L=6m,已知传送带的速度v=2m/s,物块与传送带间的动摩擦因数μ=0.2重力加速度g取1 0m/S2.关于物块在传送带上的运动,下列表述正确的是( )
如图所示,质量m=l kg的物块,以速度v0=4m/s滑上正沿逆时针转动的水平传送带,传送带上A、B两点间的距离L=6m,已知传送带的速度v=2m/s,物块与传送带间的动摩擦因数μ=0.2重力加速度g取1 0m/S2.关于物块在传送带上的运动,下列表述正确的是( )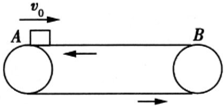
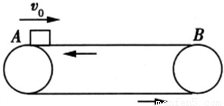 如图所示,质量m=l kg的物块,以速度v=4m/s滑上正沿逆时针转动的水平传送带,传送带上A、B两点间的距离L=6m,已知传送带的速度v=2m/s,物块与传送带间的动摩擦因数μ=0.2重力加速度g取1 0m/S2.关于物块在传送带上的运动,下列表述正确的是( )
如图所示,质量m=l kg的物块,以速度v=4m/s滑上正沿逆时针转动的水平传送带,传送带上A、B两点间的距离L=6m,已知传送带的速度v=2m/s,物块与传送带间的动摩擦因数μ=0.2重力加速度g取1 0m/S2.关于物块在传送带上的运动,下列表述正确的是( )