Question

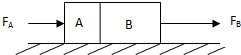在光滑水平面上放着紧靠在一起的AB两物体，B的质量是A的2倍，B受到向右的恒力F_B=2N，A受到的水平力F_A=（9-2t）N，（t的单位是s）．从t=0开始计时，则（　　）

A．A物体在2s末时刻的加速度是初始时刻的5/11倍

B．t＞4s后，B物体做匀加速直线运动

C．t=4.5s时，A物体的速度为零

D．t＞4.5s后，AB的加速度方向相反

Answer 1

分析：对整体，根据牛顿第二定律求出加速度的表达式，得到A物体在2s末时刻的加速度是初始时刻的倍数；
对B研究，由牛顿第二定律求出A对B的作用力N表达式，当N=0时，求出时间，此后A分离，B做匀加速运动；
t=4.5s时，对A，根据牛顿第二定律求出加速度，分析其速度；

解答：解：设A的质量为m，则B的质量为2m，在两物体没有分离时，对整体：根据牛顿第二定律得：
a=

FA+FB

3m

=

11-2t

3m

…①
以B为研究对象，设A对B的作用力大小为N，则有：
N+F_B=2ma…②
解得：N=

1

3

（16-4t）…③
A、由③得，当t=4s时，N=0，此后A、B分离，B物体做匀加速直线运动．当t=0时，a₁=

11

3m

；当t=2s时，a₂=

7

3m

，故A错误，B正确；
C、t=4.5s时，A的加速度为：a_A=

FA

m

=0，在4.5s之前，物体一直在做加速运动，速度不可能为零；故C错误；
D、t＞4.5s后，A的加速度a_A＜0，而B的加速度不变，则知t＞4.5s后，AB的加速度方向相反．故D正确．
故选：BD．

点评：本题是连接体问题，采用整体法和隔离法，根据牛顿第二定律得到加速度与时间的关系是关键．同时注意函数关系的正确应用．