题目内容
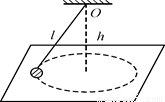
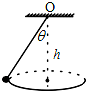 如图所示的圆锥摆,摆线与竖直方向的夹角为θ,悬点O到圆轨道平面的高度为h,下列说法正确的是( )
如图所示的圆锥摆,摆线与竖直方向的夹角为θ,悬点O到圆轨道平面的高度为h,下列说法正确的是( )分析:分析小球的受力:受到重力、绳的拉力,二者的合力提供向心力,向心力是效果力,不能分析物体受到向心力.然后用力的合成求出向心力:mgtanθ,用牛顿第二定律列出向心力的表达式,求出线速度v和周期T的表达式,分析θ变化,由表达式判断V、T的变化.
解答:解:A、向心力大小为:Fn=mgtanθ,小球做圆周运动的半径为:R=Lsinθ,则由牛顿第二定律得:mgtanθ=mω2Lsinθ,摆球质量的变化,不影响h值,故A错误;
B、由牛顿第二定律得:mgtanθ=mω2Lsinθ,得到线速度:ω=
,当ω越大,则cosθ越小,因此θ越大,则h也越小,故B正确,C错误.
D:小球运动周期:T=
=2π
,因此,θ越大,小球运动的周期越小,与摆球的质量无关,故D选项正确.
故选:BD.
B、由牛顿第二定律得:mgtanθ=mω2Lsinθ,得到线速度:ω=
|
D:小球运动周期:T=
| 2πr |
| v |
|
故选:BD.
点评:理解向心力:是效果力,它由某一个力或几个力的合力提供,它不是性质的力,分析物体受力时不能分析向心力.同时,还要清楚向心力的不同的表达式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
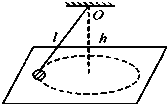 如图所示的圆锥摆,摆线与竖直方向的夹角为θ,悬点O到圆轨道平面的高度为h,下列说法正确的是( )
如图所示的圆锥摆,摆线与竖直方向的夹角为θ,悬点O到圆轨道平面的高度为h,下列说法正确的是( )| A、摆球质量越大,则h越大 | B、角速度ω越大,则摆角θ也越大 | C、角速度ω越大,则h也越大 | D、摆球周期与质量有关 |
如图所示的圆锥摆,摆线与竖直方向的夹角为θ,悬点O到圆轨道平面的高度为h,下列说法正确的是 ( )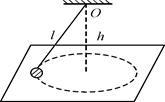
| A.摆球质量越大,则h越大 |
| B.角速度ω越大,则摆角θ也越大 |
| C.角速度ω越大,则h也越大 |
| D.摆球周期与质量有关 |
 如图所示的圆锥摆,摆线与竖直方向的夹角为θ,悬点O到圆轨道平面的高度为 h,下列关于物体受力说法正确的是( )
如图所示的圆锥摆,摆线与竖直方向的夹角为θ,悬点O到圆轨道平面的高度为 h,下列关于物体受力说法正确的是( )