题目内容
如图1所示,在x轴上0到d范围内存在电场(图中未画出),x轴上各点的电场沿着x轴正方向,并且电场强度大小E随x的分布如图2所示;在x轴上d到2d范围内存在垂直纸面向里的匀强磁场,磁感应强度大小为B.一质量为m,电量为+q粒子沿x轴正方向以一定速度从O点进入电场,最终粒子恰从坐标为(2d, )的P点离开磁场.不计粒子重力.
)的P点离开磁场.不计粒子重力.(1)求在x=0.5d处,粒子的加速度大小a;
(2)求粒子在磁场中的运动时间t;
(3)类比是一种常用的研究方法.对于直线运动,教科书中讲解了由v-t图象求位移的方法.请你借鉴此方法,并结合其他物理知识,求电场对粒子的冲量大小I.

【答案】分析:(1)从图象中得出x=0.5d处的电场强度,根据牛顿第二定律求出粒子的加速度大小.
(2)根据几何关系得出粒子在磁场中做匀速圆周运动的轨道半径和圆心角的大小,根据 ,结合周期公式求出粒子在磁场中运动的时间.
,结合周期公式求出粒子在磁场中运动的时间.
(3)根据粒子在磁场中的轨道半径,结合轨道半径的公式求出粒子进入磁场的速度,根据图象求出电场力做功W= .根据动能定理求出带电粒子进入电场时的速度,最后根据动量定理求出电场对粒子的冲量大小I.
.根据动能定理求出带电粒子进入电场时的速度,最后根据动量定理求出电场对粒子的冲量大小I.
解答:解:(1)由图象,x=0.5d处,电场强度为E=0.5E,由牛顿第二定律得:
qE=ma
解得: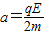 .
.
(2)在磁场中运动轨迹如图,设半径为R,由几何关系

解得:R= .
.
设圆弧所对圆心为α,满足:sin
解得: .
.
粒子在磁场中做圆周运动,设在磁场中运动的周期为T,粒子在磁场的运动速率为v,
圆运动半径为 R,根据牛顿第二定律:
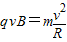
粒子运动的周期 .
.
所以,粒子在磁场中运动时间 .
.
(3)粒子在磁场中做圆周运动,由牛顿第二定律得:
 ,又粒子做圆周运动的半径R=
,又粒子做圆周运动的半径R= .
.
解得粒子在磁场中的运动速度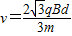 .
.
由图象可知,电场中电场力对粒子做功W= .
.
设粒子刚进入电场时速度为v,根据动能定理: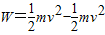 .
.
解得: =
= .
.
根据动量定理:
 .
.
答:(1)在x=0.5d处,粒子的加速度大小为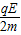 .
.
(2)粒子在磁场中的运动时间为 .
.
(3)电场对粒子的冲量大小为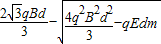 .
.
点评:解决本题的关键掌握带电粒子在磁场中运动的半径公式和周期公式,掌握求粒子在磁场中运动时间的方法,以及知道图线与横轴围成的面积再乘以电量为电场力所做的功.
(2)根据几何关系得出粒子在磁场中做匀速圆周运动的轨道半径和圆心角的大小,根据
 ,结合周期公式求出粒子在磁场中运动的时间.
,结合周期公式求出粒子在磁场中运动的时间.(3)根据粒子在磁场中的轨道半径,结合轨道半径的公式求出粒子进入磁场的速度,根据图象求出电场力做功W=
 .根据动能定理求出带电粒子进入电场时的速度,最后根据动量定理求出电场对粒子的冲量大小I.
.根据动能定理求出带电粒子进入电场时的速度,最后根据动量定理求出电场对粒子的冲量大小I.解答:解:(1)由图象,x=0.5d处,电场强度为E=0.5E,由牛顿第二定律得:
qE=ma
解得:
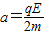 .
.(2)在磁场中运动轨迹如图,设半径为R,由几何关系

解得:R=
 .
.设圆弧所对圆心为α,满足:sin

解得:
 .
.粒子在磁场中做圆周运动,设在磁场中运动的周期为T,粒子在磁场的运动速率为v,
圆运动半径为 R,根据牛顿第二定律:
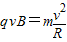
粒子运动的周期
 .
.所以,粒子在磁场中运动时间
 .
.(3)粒子在磁场中做圆周运动,由牛顿第二定律得:
 ,又粒子做圆周运动的半径R=
,又粒子做圆周运动的半径R= .
.解得粒子在磁场中的运动速度
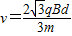 .
.由图象可知,电场中电场力对粒子做功W=
 .
.设粒子刚进入电场时速度为v,根据动能定理:
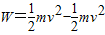 .
.解得:
 =
= .
.根据动量定理:

 .
.答:(1)在x=0.5d处,粒子的加速度大小为
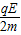 .
.(2)粒子在磁场中的运动时间为
 .
.(3)电场对粒子的冲量大小为
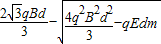 .
.点评:解决本题的关键掌握带电粒子在磁场中运动的半径公式和周期公式,掌握求粒子在磁场中运动时间的方法,以及知道图线与横轴围成的面积再乘以电量为电场力所做的功.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图1所示,在x轴上0到d范围内存在电场(图中未画出),x轴上各点的电场沿着x轴正方向,并且电场强度大小E随x的分布如图2所示;在x轴上d到2d范围内存在垂直纸面向里的匀强磁场,磁感应强度大小为B.一质量为m,电量为+q粒子沿x轴正方向以一定速度从O点进入电场,最终粒子恰从坐标为(2d,
如图1所示,在x轴上0到d范围内存在电场(图中未画出),x轴上各点的电场沿着x轴正方向,并且电场强度大小E随x的分布如图2所示;在x轴上d到2d范围内存在垂直纸面向里的匀强磁场,磁感应强度大小为B.一质量为m,电量为+q粒子沿x轴正方向以一定速度从O点进入电场,最终粒子恰从坐标为(2d,
 的粒子沿x轴正方向以某一初速度从O点进入电场,最终粒子恰从坐标为(2d,
的粒子沿x轴正方向以某一初速度从O点进入电场,最终粒子恰从坐标为(2d, )的P点离开磁场。不计粒子重力。
)的P点离开磁场。不计粒子重力。
 的粒子沿x轴正方向以某一初速度从O点进入电场,最终粒子恰从坐标为(2d,
的粒子沿x轴正方向以某一初速度从O点进入电场,最终粒子恰从坐标为(2d, )的P点离开磁场。不计粒子重力。
)的P点离开磁场。不计粒子重力。