题目内容
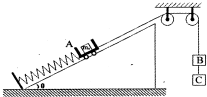 如图所示,一轻质弹簧下端与固定挡板相连,上端与放在倾角θ=30°的光滑斜面上的小车A相接触(未连接).小车A质量M=3kg,内有质量m0=1kg的砝码,小车A又与一跨过定滑轮的不可伸长的轻绳一端相连,绳另一端悬挂着物体B,B的下面又挂着物体C,B和C质量均为m=1kg,A、B、C均处于静止状态.现剪断B和C之间的绳子,则A和B开始做振幅为d=5cm的简谐运动,斜面足够长且始终静止.(g取10m/s2)试求:
如图所示,一轻质弹簧下端与固定挡板相连,上端与放在倾角θ=30°的光滑斜面上的小车A相接触(未连接).小车A质量M=3kg,内有质量m0=1kg的砝码,小车A又与一跨过定滑轮的不可伸长的轻绳一端相连,绳另一端悬挂着物体B,B的下面又挂着物体C,B和C质量均为m=1kg,A、B、C均处于静止状态.现剪断B和C之间的绳子,则A和B开始做振幅为d=5cm的简谐运动,斜面足够长且始终静止.(g取10m/s2)试求:(1)剪断绳子的瞬间小车A的加速度大小;
(2)剪断绳子后弹簧的最大弹性势能;
(3)当小车A运动到最低点时,取走小车内的砝码,此后小车A沿斜面上滑的最大距离.
分析:(1)该问属于瞬时加速度问题,注意剪断绳子瞬间,绳子上的力发生突变,但是弹簧上的力不发生改变,明确这点根据牛顿第二定律即可求解.
(2)根据简谐运动特点可知:当系统动能为零时,弹性势能最大,依据功能关系可解得结果.
(3)当小车A运动到最低点后将沿斜面上滑,弹簧弹性势能和m重力势能减小,转化为小车的重力势能,明确过程中的功能关系即可正确解答.
(2)根据简谐运动特点可知:当系统动能为零时,弹性势能最大,依据功能关系可解得结果.
(3)当小车A运动到最低点后将沿斜面上滑,弹簧弹性势能和m重力势能减小,转化为小车的重力势能,明确过程中的功能关系即可正确解答.
解答:解:(1)绳子剪短前,由于(M+m0)gsin30°=2mg,弹簧没有弹力.则绳子剪短瞬间:
对A受力分析得:(M+m0)gsin300 -T=(M+m)a ①
对B受力分析得:T-mg=ma ②
联立①②解得:a=2m/s2.
故剪断绳子的瞬间小车A的加速度大小为2m/s2.
(2)当弹簧被压缩2d时弹性势能最大,由功能关系得:
(M+m)g?2dsin30°=mg?2d+Epm
解得:EPm=1J
故剪断绳子后弹簧的最大弹性势能EPm=1J.
(3)当小车滑行道最高点时,A、B的速度均为0,由系统功能关系得:
Epm=Mgssin300-mgs
解得:s=0.2m.
故此后小车A沿斜面上滑的最大距离为0.2m.
对A受力分析得:(M+m0)gsin300 -T=(M+m)a ①
对B受力分析得:T-mg=ma ②
联立①②解得:a=2m/s2.
故剪断绳子的瞬间小车A的加速度大小为2m/s2.
(2)当弹簧被压缩2d时弹性势能最大,由功能关系得:
(M+m)g?2dsin30°=mg?2d+Epm
解得:EPm=1J
故剪断绳子后弹簧的最大弹性势能EPm=1J.
(3)当小车滑行道最高点时,A、B的速度均为0,由系统功能关系得:
Epm=Mgssin300-mgs
解得:s=0.2m.
故此后小车A沿斜面上滑的最大距离为0.2m.
点评:该题运动过程复杂为变速运动,但是如果把握过程中功能转化关系,抓住功能这条主线即可化难为简,因此在今后练习中要加强功能关系的应用.

练习册系列答案
相关题目
 如图所示,一轻质弹簧竖直放置,下端固定在水平面上,上端处于a位置.当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置.现将重球(视为质点)轻放在弹簧a处,由静止释放后,球沿弹簧中轴线向下运动到最低点c处的过程中,下列说法正确的是( )
如图所示,一轻质弹簧竖直放置,下端固定在水平面上,上端处于a位置.当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置.现将重球(视为质点)轻放在弹簧a处,由静止释放后,球沿弹簧中轴线向下运动到最低点c处的过程中,下列说法正确的是( ) 如图所示,一轻质弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点,已知OC=h,振子的周期为T.某时刻物体恰好经过C点并向上运动,则从此时刻开始的半个周期时间内,下列判断正确的是( )
如图所示,一轻质弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点,已知OC=h,振子的周期为T.某时刻物体恰好经过C点并向上运动,则从此时刻开始的半个周期时间内,下列判断正确的是( ) 如图所示,一轻质弹簧固定在水平地面上,O点为弹簧原长时上端的位置,一个质量为m的物体从O点正上方的A点由静止释放落到弹簧上,物体压缩弹簧到最低点B 后向上运动.则以下说法正确的是( )
如图所示,一轻质弹簧固定在水平地面上,O点为弹簧原长时上端的位置,一个质量为m的物体从O点正上方的A点由静止释放落到弹簧上,物体压缩弹簧到最低点B 后向上运动.则以下说法正确的是( )