Question

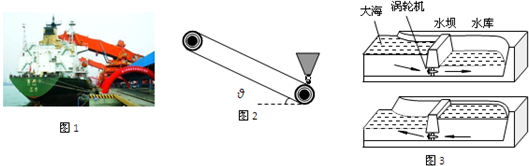
“潮汐发电”是海洋能利用中发展最早、规模最大、技术较成熟的一种方式。某海港的货运码头，就是利用“潮汐发电”为皮带式传送机供电，图1所示为皮带式传送机往船上装煤。本题计算中取sin18^o=0.31，cos18^o=0.95，水的密度ρ =1.0×10³kg/m³，g=10m/s²。

（1）皮带式传送机示意图如图2所示, 传送带与水

平方向的角度θ = 18^o，传送带的传送距离为L = 51.8m，它始终以v = 1.4m/s的速度运行。在传送带的最低点，漏斗中的煤自由落到传送带上（可认为煤的初速度为0），煤与传送带之间的动摩擦因数μ = 0.4。求：从煤落在传送带上到运至传送带最高点经历的时间t；

（2）图3为潮汐发电的示意图。左侧是大海，中间

有水坝，水坝下装有发电机，右侧是水库。当涨潮到海平面最高时开闸，水由通道进入海湾水库，发电机在水流的推动下发电，待库内水面升至最高点时关闭闸门；当落潮到海平面最低时，开闸放水发电。设某潮汐发电站发电有效库容V =3.6×10 ⁶m³，平均潮差Δh = 4.8m，一天涨落潮两次，发电四次。水流发电的效率η₁ = 10％。求该电站一天内利用潮汐发电的平均功率P；

（3）传送机正常运行时，1秒钟有m = 50kg的煤从漏斗中落到传送带上。带动传送带的电动机将输入电能转化为机械能的效率η₂ = 80%，电动机输出机械能的20%用来克服传送带各部件间的摩擦（不包括传送带与煤之间的摩擦）以维持传送带的正常运行。若用潮汐发电站发出的电给传送机供电，能同时使多少台这样的传送机正常运行？

Answer 1

（1）  38s     （2）400kW     （3）30台

解析:

：（1）煤在传送带上的受力如右图所示  （1分）

        根据牛顿第二定律  μm′gcosθ– m′gsinθ = m′a      （1分）

        设煤加速到v需要时间为t₁    v = at₁       t₁ = 2s   （1分）

         设煤加速运动的距离为s₁    v² = 2as₁      s₁ = 1.4m （1分）

        设煤匀速运动的时间为t₂  L – s₁ = vt₂      t₂ = 36s　（1分）

        总时间                 t = t₁ + t₂ = 38s          （1分）

   （2）一次发电，水的质量    M = ρV = 3.6×10⁹kg       （1分）

               重力势能减少    E_P = Mg            （1分）

        一天发电的能量        E = 4 E_P×10 %     （2分）

        平均功率                         （1分）

        求出                 P = 400kW         （1分）

   （3）一台传送机，将1秒钟内落到传送带上的煤送到传送带上的最高点

煤获得的机械能为  E_机=          （1分）

        传送带与煤之间因摩擦产生的热 Q =      （1分）

        煤与传送带的相对位移        m    （1分）

        设同时使n台传送机正常运行，根据能量守恒

            P×80%×80% = n（+）（3分）

        求出                 n = 30台             　       （2分）

        评分标准：若仅列出一个能量守恒方程，方程全对给5分，若方程有错均不给分。