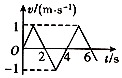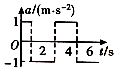��Ŀ����
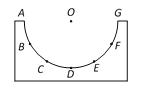
����Ŀ����ͼ��ʾ��ֱ������ϵxOyλ��ͬһ��ֱƽ���ڣ�����x��ˮƽ��y����ֱ��xOyƽ���ڳ���������OABC���з���ֱOA����ǿ�糡��OA��Ϊl����x���ļн�=30����һ����Ϊm�������Ϊq�Ĵ�����С�ɿ����ʵ㣩��y���ϵ�P����x�᷽����һ���ٶ������ǡ�ô�OA���е�M��ֱOA���˵糡������֪�������ٶ�Ϊg��
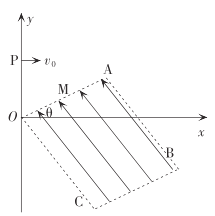
��1����P��������꼰С���P�����ʱ���ٶ�v0��
��2����֪�糡ǿ�ȵĴ�СΪE=![]() ����С���ܴ�BC�߽��뿪�糡��OC����Ӧ����ʲô������
����С���ܴ�BC�߽��뿪�糡��OC����Ӧ����ʲô������
���𰸡���1��![]() ��
�� ![]() ��2��
��2��![]()
�����������������С���P��M��ƽ���˶�������ƽ���˶��Ĺ��ɼ����ι�ϵ�������������yp��С��ij��ٶȣ������˶��ĺϳ���ֽ⣬�������ֽ�Ϊ��ֱ�ڵ糡�ߺ�ƽ���ڵ糡�ߣ��ɵ��ص糡�ߺ���Ϊ0��������ֱ���˶�����ֱ�糡�߸���ţ�ٵڶ�����������ٶȣ������˶�ѧ�����г�����������˶�ѧ���̼��ɡ�
��1����С���P��M����ʱ��Ϊt1
����ֱ���������������˶��� ![]()
��ˮƽ���� ![]()
�ɼ��ι�ϵ�� ![]()
�����ɵã� ![]()
![]()
��2����С��Mʱ�ٶ�ΪvM���ɼ��ι�ϵ�� ![]()
����ƽ�������ã� ![]()
С���ڵ糡����vM��������ֱ���˶�������vM��ֱ���������ٶ�Ϊa���ȼ����˶�����߽�OC�ij���Ϊdʱ��С��BC��������ڵ糡���˶�ʱ��Ϊt2
��ţ�ٵڶ����ɵã�mgsin300=ma
��ã�a=5m/s2
λ�ƹ�ϵΪ�� ![]()
![]()
�����ɵã� ![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�