题目内容
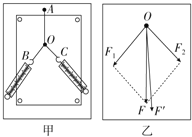
【题目】如图所示,一半径为R的球体绕轴O1O2以角速度ω匀速转动,A、B为球体上两点。下列说法中正确的是( )

A.A、B两点具有相同的角速度
B.A、B两点具有相同的线速度
C.A、B两点具有相同的向心加速度
D.A、B两点的向心加速度方向都指向球心
【答案】A
【解析】A、B两点随球体一起绕轴O1O2转动,转一周所用的时间相等,故角速度相等,有ωA=ωB=ω,选项A正确;A点做圆周运动的平面与轴O1O2垂直,交点为圆心,故A点做圆周运动的半径为rA=Rsin60°;同理,B点做圆周运动的半径为rB=Rsin30°,所以A、B两点的线速度分别为:vA=rAω=![]() Rω,vB=rBω=
Rω,vB=rBω=![]() Rω,显然vA>vB,选项B错误;A、B两点的向心加速度分别为:aA=rAω2=
Rω,显然vA>vB,选项B错误;A、B两点的向心加速度分别为:aA=rAω2=![]() Rω2,aB=rBω2=
Rω2,aB=rBω2=![]() Rω2,显然,A、B两点的向心加速度不相等,且它们的向心加速度方向均指向各自平面的圆心,并不指向球心,故选项C、D错误。
Rω2,显然,A、B两点的向心加速度不相等,且它们的向心加速度方向均指向各自平面的圆心,并不指向球心,故选项C、D错误。

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目