题目内容
4.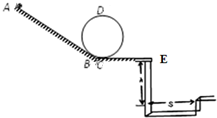 某校物理兴趣小组举行玩具赛车比赛.比赛路径如图所示,粗糙斜面轨道AB与半径R=0.32m的光滑竖直圆轨道及光滑水平轨道CE相连,圆轨道相切于B、C两点(两点间距不计),赛车从起点A静止出发,沿斜面轨道运动L后,进入竖直圆轨道(不能脱离轨道),离开竖直圆轨道后继续在光滑平直轨道上运动到E点,并能越过壕沟.已知斜面倾斜角30°,赛车质量m=0.1kg,在粗糙斜面轨道AB段受到阻力恒为0.1N.图中壕沟两岸高度差h=1.25m,沟宽S=1.50m.(取g=10m/s2).求:
某校物理兴趣小组举行玩具赛车比赛.比赛路径如图所示,粗糙斜面轨道AB与半径R=0.32m的光滑竖直圆轨道及光滑水平轨道CE相连,圆轨道相切于B、C两点(两点间距不计),赛车从起点A静止出发,沿斜面轨道运动L后,进入竖直圆轨道(不能脱离轨道),离开竖直圆轨道后继续在光滑平直轨道上运动到E点,并能越过壕沟.已知斜面倾斜角30°,赛车质量m=0.1kg,在粗糙斜面轨道AB段受到阻力恒为0.1N.图中壕沟两岸高度差h=1.25m,沟宽S=1.50m.(取g=10m/s2).求:(1)赛车越过壕沟需要的最小速度为v1
(2)要使赛车顺利完成全部比赛,斜面AB段最小长度L.
分析 本题赛车的运动可以分为三个过程,由A至B的过程可以运用动能定理列式,在圆轨道上的过程机械能守恒,也可以用动能定理列式,以及平抛运动的过程;本题有两个约束条件,即要能越过壕沟,同时要能到达轨道的最高点.
解答 解:(1)设赛车越过壕沟需要的最小速度为v1,由平抛运动的规律,有:
S=v1t
$h=\frac{1}{2}g{t}^{2}$
解得:
${v}_{1}=S\sqrt{\frac{R}{2h}}=3m/s$
(2)设赛车恰好越过圆轨道,对应圆轨道最高点的速度为v2,最低点的速度为v3,
由牛顿第二定律:mg=m$\frac{{v}_{2}^{2}}{R}$
由动能定理:$-mg2R=\frac{1}{2}mv_2^2-\frac{1}{2}mv_3^2$
解得:
${v}_{3}=\sqrt{5gh}$=4m/s
通过分析比较,赛车要完成比赛,在进入圆轨道前的速度最小应该是4m/s
赛车在斜面轨道AB,根据动能定理,有:$mgLsin{30^0}-fL=\frac{1}{2}mv_{min}^2-0$
可得:L=2m
答:(1)赛车越过壕沟需要的最小速度为为3m/s;
(2)要使赛车顺利完成全部比赛,斜面AB段最小长度L为2m.
点评 本题是力电综合问题,关键要将物体的运动分为三个过程,分析清楚各个过程的运动特点和受力特点,然后根据动能定理、平抛运动公式、向心力公式列式求解!

练习册系列答案
相关题目
15.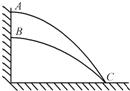 某同学在网球训练中,网球在不同高度A、B处与竖直墙壁碰撞后,垂直墙面弹出,均落在水平地面上的C处,如图所示.若网球弹出时速度大小分别为vA、vB,从弹出到落地的时间分别为tA、tB,则( )
某同学在网球训练中,网球在不同高度A、B处与竖直墙壁碰撞后,垂直墙面弹出,均落在水平地面上的C处,如图所示.若网球弹出时速度大小分别为vA、vB,从弹出到落地的时间分别为tA、tB,则( )
 某同学在网球训练中,网球在不同高度A、B处与竖直墙壁碰撞后,垂直墙面弹出,均落在水平地面上的C处,如图所示.若网球弹出时速度大小分别为vA、vB,从弹出到落地的时间分别为tA、tB,则( )
某同学在网球训练中,网球在不同高度A、B处与竖直墙壁碰撞后,垂直墙面弹出,均落在水平地面上的C处,如图所示.若网球弹出时速度大小分别为vA、vB,从弹出到落地的时间分别为tA、tB,则( )| A. | tA=tB | B. | tA<tB | C. | vA=vB | D. | vA<vB |
12.如图所示,原、副线圈匝数比为2:1的理想变压器正常工作时( )


| A. | 原、副线圈磁通量之比为2:1 | B. | 原、副线圈磁通量变化率之比为2:1 | ||
| C. | 输入功率和输出功率之比为1:1 | D. | 原、副线圈电流之比为1:2 |
19.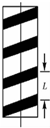 在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )
在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )
 在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )
在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )| A. | 顺时针 转速n=$\frac{v}{2πL}$ | B. | 顺时针 转速n=$\frac{v}{L}$ | ||
| C. | 逆时针 转速n=$\frac{v}{2πL}$ | D. | 逆时针 转速n=$\frac{v}{L}$ |
9.两个物体分别做平抛运动落到同一水平面上,如果它们的水平分位移相等,则( )
| A. | 它们的初速度一定相等 | |
| B. | 它们抛出时的高度一定相等 | |
| C. | 它们在空中运动的时间一定相等 | |
| D. | 它们的初速度v0与高度的平方根$\sqrt{h}$的乘积一定相等 |
16.河宽为d,水流速度为v1,船在静水中的速度为v2,要使船在渡河过程中通过位移s最短,则下列说法正确的是( )
| A. | v1>v2时,s=d | B. | v1<v2时,s<d | C. | v1>v2时,s>d | D. | v1<v2时,s=d |
13.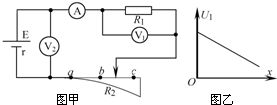 电阻非线性变化的滑动变阻器R2接入图甲的电路中,移动滑动变阻器触头改变接入电路中的长度x(x为图中a与触头之间的距离),定值电阻R1两端的电压U1与x间的关系如图乙,a、b、c为滑动变阻器上等间距的三个点,当触头从a移到b和从b移到c的这两过程中,下列说法正确的是( )
电阻非线性变化的滑动变阻器R2接入图甲的电路中,移动滑动变阻器触头改变接入电路中的长度x(x为图中a与触头之间的距离),定值电阻R1两端的电压U1与x间的关系如图乙,a、b、c为滑动变阻器上等间距的三个点,当触头从a移到b和从b移到c的这两过程中,下列说法正确的是( )
 电阻非线性变化的滑动变阻器R2接入图甲的电路中,移动滑动变阻器触头改变接入电路中的长度x(x为图中a与触头之间的距离),定值电阻R1两端的电压U1与x间的关系如图乙,a、b、c为滑动变阻器上等间距的三个点,当触头从a移到b和从b移到c的这两过程中,下列说法正确的是( )
电阻非线性变化的滑动变阻器R2接入图甲的电路中,移动滑动变阻器触头改变接入电路中的长度x(x为图中a与触头之间的距离),定值电阻R1两端的电压U1与x间的关系如图乙,a、b、c为滑动变阻器上等间距的三个点,当触头从a移到b和从b移到c的这两过程中,下列说法正确的是( )| A. | 电流表A示数变化相等 | B. | 电压表V2的示数变化不相等 | ||
| C. | 电阻R1的功率变化相等 | D. | 电源的输出功率均不断增大 |
14.一质量为m的木块静止在光滑的水平面上,从t=0开始,将一个大小为F的水平恒力作用在该木块上,在t=t1时刻物体的( )
| A. | 速度为$\frac{F{t}_{1}}{m}$ | B. | 速度为$\frac{F{t}_{1}}{2m}$ | ||
| C. | 动能为$\frac{{F}^{2}{t}_{1}}{2m}$ | D. | 动能为$\frac{{F}^{2}{{t}_{1}}^{2}}{2m}$ |