题目内容
10．
如图所示，一两端开口的细长试管插入一封闭容器中，试管内外的液面有高度差，管内液面高度为H，管内液面到容器底部的距离为h，若将底部阀门打开，瞬间水流喷出时的速率为$\sqrt{2gh}$（阀门高度远小于h）
分析 由平衡条件求出容器内气体的压强，
由牛顿第二定律求出打开阀门时水的加速度，
然后应用匀变速运动的速度位移公式求出水的速度．
解答 解：设大气压为：p0，容器内气体压强为：p，
则：p+ρg（H-h）=p0 ①
设阀门的面积为S，打开阀门瞬间有长度为L的水喷出，由于时间很短，喷出的水可以认为做初速度为零的匀加速直线运动，
水的质量：m=ρSL ②，
对喷出的水，由牛顿第二定律得：pS-p0S=ma ③，
由匀变速直线运动的速度位移公式得：v2=2aL ④，
由①②③④解得：v=$\sqrt{2gh}$；
故答案为：$\sqrt{2gh}$．
点评 本题考查了求水喷出时的速度，求出封闭气体压强、应用牛顿第二定律、运动学公式可以解题，本题也可以应用动能定理求解，解题时要注意微元法的应用．
练习册系列答案
阅读快车系列答案
相关题目
20．下列说法中正确的是（ ）
| A． | 气体的温度升高时，每个分子的运动速度增大，分子的平均动能一定增大 | |
| B． | 布朗运动是悬浮在液体中的小微粒做无规则运动，反映了液体分子做无规则运动 | |
| C． | 两块纯净铅压紧以后能连成一块，说明分子间只存在引力 | |
| D． | 当分子间距离增大时，分子间引力和斥力都减小，而分子势能增大 |
如图所示，在竖直平面内固定着半径为R的光滑的$\frac{1}{4}$圆弧槽，它的末端水平，上端离地面高H，一个小球从上端无初速度下滑，求：
从高度y=20m处以某一初速度水平抛出一物体，落到水平地面时的水平位移为x=6m，（g取10m/s2，不考虑空气助力）求：
15．
木块A和B置于水平面上，它们的质量分别为ma和mb，与水平面的动摩擦因素都为μ．如图所示当水平力F作用于左端A上，两个物体一起加速运动时，AB间的作用力大小为N1．当同样大小的力F水平作用于右端B上，两物体一起加速运动时，AB间作用力大小为N2，则（ ）
木块A和B置于水平面上，它们的质量分别为ma和mb，与水平面的动摩擦因素都为μ．如图所示当水平力F作用于左端A上，两个物体一起加速运动时，AB间的作用力大小为N1．当同样大小的力F水平作用于右端B上，两物体一起加速运动时，AB间作用力大小为N2，则（ ）| A． | N1+N2＞F | B． | N1+N2＜F | C． | N1+N2=F | D． | N1：N2=ma：mb |
2．A、B两个物体从同一地点开始在同一直线上做匀变速运动，它们的速度-时间图象如图所示，则（ ）
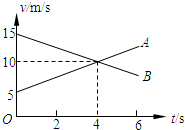
| A． | A、B两个物体的运动方向相反 | B． | t=4s时，两物体相遇 | ||
| C． | t=4s时，两物体距离最小 | D． | 相遇前，两物体最大距离为20m |
如图所示，将质量均为m厚度不计的两物块A、B用轻质弹簧相连接．第一次只用手托着B物块于H高处，A在弹簧弹力的作用下处于静止，现将弹簧锁定，此时弹簧的弹性势能为Ep，现由静止释放A、B，B物块着地后速度立即变为0，同时弹簧锁定解除，在随后的过程中B物块恰能离开地面但不继续上升．第二次用手拿着A、B两物块，使得弹簧竖直并处于原长状态，此时物块B离地面的距离也为H，然后由静止同时释放A、B，B物块着地后速度同样立即变为0．求：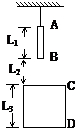
如图所示，悬挂的直杆AB长为L1=10米，在其下L2=5米处，有一长为L3=5米的无底圆筒CD，若将悬线剪断，则直杆穿过圆筒所用的时间为多少？