题目内容
11. 如图所示,足够深的水池中,有一个木球A与一个空心铁球B,质量分别为m、M,体积相同,由一根不可伸长的细线相连.开始时用手托住A,松手使A从O点开始由静止下落,加速度大小为a,经过一段时间,A经过P点,此时细线断开,又经过相同时间,A恰好经过OP的中点(忽略水的阻力),下列说法正确的是( )
如图所示,足够深的水池中,有一个木球A与一个空心铁球B,质量分别为m、M,体积相同,由一根不可伸长的细线相连.开始时用手托住A,松手使A从O点开始由静止下落,加速度大小为a,经过一段时间,A经过P点,此时细线断开,又经过相同时间,A恰好经过OP的中点(忽略水的阻力),下列说法正确的是( )| A. | 细线断开后,A处于失重状态 | |
| B. | A受到的浮力大小F=$\frac{(m+M)}{2}$(g-a) | |
| C. | 细线断开后,A球的加速度大小为$\frac{5}{2}$a | |
| D. | 细线断开前,张力大小为FT=$\frac{(m+M)}{2}$(g-a) |
分析 根据A球的加速度方向确定A处于超重还是失重状态.对整体分析,根据牛顿第二定律求出整体的浮力大小,从而求出A球的浮力,隔离对A球分析,根据牛顿第二定律求出细线的张力大小.根据运动学公式,抓住时间相等,结合位移关系求出A球的加速度大小.
解答 解:A、细线烧断后,A向下运动后又返回,可知A的加速度方向向上,A处于超重状态,故A错误.
B、对整体分析,(M+m)g-F浮=(M+m)a,解得整体的浮力F浮=(M+m)(g-a),由于两球的体积相同,则浮力相等,所以A受到的浮力$F=\frac{(M+m)(g-a)}{2}$,隔离对A分析,根据牛顿第二定律得mg+FT-F=ma,解得${F}_{T}=\frac{(M-m)(g-a)}{2}$,故B正确,D错误.
C、A球到P点的过程中有:L=$\frac{1}{2}a{t}^{2}$,此时A的速度v=at,又经过相同时间,A恰好经过OP的中点,有:$vt-\frac{1}{2}a′{t}^{2}=-\frac{L}{2}$,代入解得$a′=\frac{5}{2}a$,故C正确.
故选:BC.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,掌握判断超失重的方法,关键看加速度的方向.掌握整体法和隔离法的灵活运用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
2.下列说法正确的是( )
| A. | ${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He是核衰变方程 | |
| B. | 10个${\;}_{92}^{238}$U原子核经过一个半衰期,必定有5个发生衰变 | |
| C. | 天然放射现象说明原子具有核式结构 | |
| D. | 波源的发射频率会随接收者的远离而降低 |
19. 如图所示,显微镜中常用一种静电透镜,它可以把带电粒子(不计重力)聚集在中心轴上某点.其中K为平板电极,G为中央带圆孔的另一平行金属板,图中实线为两板附近等势线.K板右侧附近有一放射源,可以向右放射平行于轴线的粒子束.则( )
如图所示,显微镜中常用一种静电透镜,它可以把带电粒子(不计重力)聚集在中心轴上某点.其中K为平板电极,G为中央带圆孔的另一平行金属板,图中实线为两板附近等势线.K板右侧附近有一放射源,可以向右放射平行于轴线的粒子束.则( )
 如图所示,显微镜中常用一种静电透镜,它可以把带电粒子(不计重力)聚集在中心轴上某点.其中K为平板电极,G为中央带圆孔的另一平行金属板,图中实线为两板附近等势线.K板右侧附近有一放射源,可以向右放射平行于轴线的粒子束.则( )
如图所示,显微镜中常用一种静电透镜,它可以把带电粒子(不计重力)聚集在中心轴上某点.其中K为平板电极,G为中央带圆孔的另一平行金属板,图中实线为两板附近等势线.K板右侧附近有一放射源,可以向右放射平行于轴线的粒子束.则( )| A. | 该装置既可以使电子汇聚,也可以使质子汇聚 | |
| B. | 被汇聚的粒子电势能增加 | |
| C. | 被汇聚的粒子动能增加 | |
| D. | 速度相同的不同种粒子,不能被汇聚于同一点 |
6.2015年1月2日13时许,哈尔滨市道外区太古街与南勋街合围地段一仓库起火,经过消防官兵和群众的合力营救,连续着了10个小时的大火终于被扑灭.设消防水龙头斜向上喷出的水恰好水平击中着火点,楼高7.2米,消防员与楼体距离为24米,则水流喷出的速度最接近(忽略水龙头离地高度及一切阻力,取g=10m/s2)( )
| A. | 12.6m/s | B. | 20m/s | C. | 23.3m/s | D. | 12m/s |
16.下列五种说法,其中正确的是( )
| A. | “用油膜法估测分子的大小”实验中油酸分子直径等于油酸溶液体积除以相应油酸膜的面积 | |
| B. |  图中当两个相邻的分子间距离为r0时,它们之间相互作用的引力和斥力大小相等 | |
| C. |  图中曲线显示了氧气分子在不同温度下的速率分布情况,由图象可以判断T2>T1 | |
| D. | 电冰箱工作时热量可以从低温物体传到高温物体,因而电冰箱工作过程不遵从热力学第二定律 | |
| E. |  图中洁净的玻璃板接触水面,要使玻璃板离开水面,拉力必须大于玻璃板的重力,其原因是水分子和玻璃分子之间存在吸引力 |
20.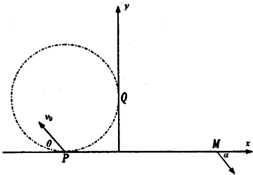 如图所示,在xOy平面的第Ⅱ象限内有半径为R的圆分别与x轴,y轴相切于P,Q两点,圆内存在垂直于xOy平面向外的匀强磁场,在第I象限内存在沿y轴负方向的匀强电场,电场强度为E.一带正电的粒子(不计重力)以速率v0从P点射入磁场后恰好垂直y轴进入电场,最后从M(3R,0)点射出电场,出射方向与x轴正方向夹角α=45°,则( )
如图所示,在xOy平面的第Ⅱ象限内有半径为R的圆分别与x轴,y轴相切于P,Q两点,圆内存在垂直于xOy平面向外的匀强磁场,在第I象限内存在沿y轴负方向的匀强电场,电场强度为E.一带正电的粒子(不计重力)以速率v0从P点射入磁场后恰好垂直y轴进入电场,最后从M(3R,0)点射出电场,出射方向与x轴正方向夹角α=45°,则( )
 如图所示,在xOy平面的第Ⅱ象限内有半径为R的圆分别与x轴,y轴相切于P,Q两点,圆内存在垂直于xOy平面向外的匀强磁场,在第I象限内存在沿y轴负方向的匀强电场,电场强度为E.一带正电的粒子(不计重力)以速率v0从P点射入磁场后恰好垂直y轴进入电场,最后从M(3R,0)点射出电场,出射方向与x轴正方向夹角α=45°,则( )
如图所示,在xOy平面的第Ⅱ象限内有半径为R的圆分别与x轴,y轴相切于P,Q两点,圆内存在垂直于xOy平面向外的匀强磁场,在第I象限内存在沿y轴负方向的匀强电场,电场强度为E.一带正电的粒子(不计重力)以速率v0从P点射入磁场后恰好垂直y轴进入电场,最后从M(3R,0)点射出电场,出射方向与x轴正方向夹角α=45°,则( )| A. | 带电粒子在磁场中运动的轨道半径为R | |
| B. | 磁场的磁感应强度大小为$\frac{E}{{v}_{0}}$ | |
| C. | 带电粒子的比荷为$\frac{{v}_{0}^{2}}{3R}$ | |
| D. | 带电粒子运动经过y轴时纵坐标值为1.5R |
1.如图甲所示,利用激光器发射出的激光照射到双缝上,在双缝后面的光屏上能呈现出明、暗相问的干涉条纹.若实验中仅改变某一个实验条件、而其他条件均不变的情况下,得到的干涉图样分别如图乙和丙所示.对于这两次实验,下列说法中正确的是( )


| A. | 由于选用的激光器不同,乙图对应的激光的频率较高 | |
| B. | 双缝到光屏的距离L不同,乙图对应的L较大 | |
| C. | 双缝的间距不同,乙图对应的间距较大 | |
| D. | 激光器到双缝的距离不同,乙图对应的距离较大 |
 如图所示,粗糙的水平面与竖直平面内的光滑弯曲轨道BC在B点相接.一小物块从AB上的D点以初速v0=8m/s出发向B点滑行,DB长为12m,物块与水平面间动摩擦因数μ=0.2,求:
如图所示,粗糙的水平面与竖直平面内的光滑弯曲轨道BC在B点相接.一小物块从AB上的D点以初速v0=8m/s出发向B点滑行,DB长为12m,物块与水平面间动摩擦因数μ=0.2,求: 如图甲所示的控制电子运动装置由偏转电场、偏转磁场组成.偏转电场处在加有电压U、相距为d的两块水平平行放置的导体板之间,匀强磁场水平宽度一定,竖直长度足够大,其紧靠偏转电场的右边.大量电子以相同初速度连续不断地沿两板正中间虚线的方向向右射入导体板之间.当两板间没有加电压时,这些电子通过两板之间的时间为2t0;当两板间加上图乙所示的电压U时,所有电子均能通过电场、穿过磁场,最后打在竖直放置的荧光屏上.已知电子的质量为m、电荷量为e,不计电子的重力及电子间的相互作用,电压U的最大值为U0,磁场的磁感应强度大小为B、方向水平且垂直纸面向里.
如图甲所示的控制电子运动装置由偏转电场、偏转磁场组成.偏转电场处在加有电压U、相距为d的两块水平平行放置的导体板之间,匀强磁场水平宽度一定,竖直长度足够大,其紧靠偏转电场的右边.大量电子以相同初速度连续不断地沿两板正中间虚线的方向向右射入导体板之间.当两板间没有加电压时,这些电子通过两板之间的时间为2t0;当两板间加上图乙所示的电压U时,所有电子均能通过电场、穿过磁场,最后打在竖直放置的荧光屏上.已知电子的质量为m、电荷量为e,不计电子的重力及电子间的相互作用,电压U的最大值为U0,磁场的磁感应强度大小为B、方向水平且垂直纸面向里.