题目内容
（2011?商丘二模）一小物块以某一初速度滑上水平足够长的固定木板，经一段时间t后停止．现将该木板改置成倾角为30°的斜面，让该小物块以相同大小的初速度沿木板上滑．若小物块与木板之间的动摩擦因数为μ，则小物块上滑到最高位置所需时间t′与t之比为（ ）
分析：先对物体受力分析，根据牛顿第二定律求出加速度，然后根据运动学公式列式求解．
解答：解：物体沿水平面滑行时，有
μmg=ma1
解得
a1=μg ①
根据速度时间公式，有
0=v-a1t ②
物体沿斜面滑行时，受到重力、支持力和摩擦力，如图
根据牛顿第二定律，有
mgsin30°+μmgcos30°=ma2
解得
a2=g（sin30°+μcos30°） ③
根据速度时间公式，有
0=v-a2t′④
由①②③④解得
=
=
=
故选B．
μmg=ma1
解得
a1=μg ①
根据速度时间公式，有
0=v-a1t ②
物体沿斜面滑行时，受到重力、支持力和摩擦力，如图
根据牛顿第二定律，有
mgsin30°+μmgcos30°=ma2
解得
a2=g（sin30°+μcos30°） ③
根据速度时间公式，有
0=v-a2t′④
由①②③④解得
| t |
| t′ |
| ||
|
| a2 |
| a1 |
| 2μ | ||
1+
|
故选B．
点评：本题关键是受力分析后，根据牛顿第二定律求出加速度，然后根据速度时间公式列式求解．
练习册系列答案
名校课堂系列答案
相关题目
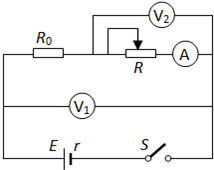（2011?商丘二模）某同学到实验室做“测电源电动势和内阻”的实验时，发现实验台上有以下器材：
（2011?商丘二模）如图所示，质量为M、半径为R、内壁光滑的半球形容器静放在粗糙水平地面上，O为球心．有一劲度系数为K的轻弹簧一端固定在半球底部O′处，另一端与质量为m的小球相连，小球静止于P点．已知地面与半球形容器间的动摩擦因数为μ，OP与水平方向的夹角为θ=30°．下列说法正确的是（ ）
