题目内容
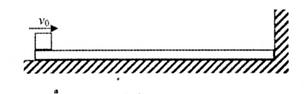
如图所示,光滑水平面上一质量为M、长为L的木板右端靠竖直墙壁。质量为m 的小滑块(可视为质点)以水平速度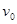 滑上木板的左端,滑到木板的右端时速度恰好为零。
滑上木板的左端,滑到木板的右端时速度恰好为零。
①求小滑块与木板间的摩擦力大小;
②现小滑块以某一速度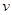 滑上木板的左端,滑到木板的右端时与竖直墙壁发生弹性碰 撞,然后向左运动,刚好能够滑到时木板左端而不从木板上落下,试求
滑上木板的左端,滑到木板的右端时与竖直墙壁发生弹性碰 撞,然后向左运动,刚好能够滑到时木板左端而不从木板上落下,试求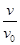 的值。
的值。
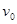 滑上木板的左端,滑到木板的右端时速度恰好为零。
滑上木板的左端,滑到木板的右端时速度恰好为零。
①求小滑块与木板间的摩擦力大小;
②现小滑块以某一速度
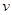 滑上木板的左端,滑到木板的右端时与竖直墙壁发生弹性碰 撞,然后向左运动,刚好能够滑到时木板左端而不从木板上落下,试求
滑上木板的左端,滑到木板的右端时与竖直墙壁发生弹性碰 撞,然后向左运动,刚好能够滑到时木板左端而不从木板上落下,试求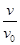 的值。
的值。 1)Ff=mv02/2 2)v/v0=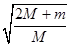
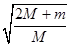
试题分析:①小滑块以水平速度v0右滑时,有:- Ff=0-mv02/2,解得Ff=mv02/2
②小滑块以速度v滑上木板到运动至碰墙时速度为v1,则有- FfL=mv12/2- mv2/2
滑块与墙碰后至向左运动到木板左端,此时滑块、木板的共同速度为v2,则有Mv1=(m+M)v2
FfL= mv12/2- (m+M)v22/2
上述四式联立,解得v/v0=
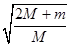

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
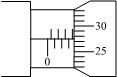
 欧姆挡,按正确的实验操作步骤测量,表盘指针位置如图所示,该电阻的阻值约为
欧姆挡,按正确的实验操作步骤测量,表盘指针位置如图所示,该电阻的阻值约为 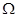 ;
;
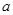 端,红表笔接
端,红表笔接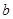 端时,指针偏转角较大,然后黑、红表笔反接指针偏转角较小,说明 (填“
端时,指针偏转角较大,然后黑、红表笔反接指针偏转角较小,说明 (填“