题目内容
13.一支队伍沿平直的公路匀速前进,其速度的大小为v1,队伍全长为L.一个通讯兵从队尾以速度v2赶到队前,(v2>v1)然后立即原速返回队尾,求这个过程中通信兵通过的路程S和位移x.分析 本题如果以地面为参考系分析较为复杂,可以以行进的队伍为参考系,可以将运动简化.
根据匀速直线运动的规律列出等式和几何关系求解.
解答 解:本题如果以地面为参考系分析较为复杂,可以以行进的队伍为参考系.在通讯兵从队尾向队前前进的过程中,通讯兵相对于队伍的速度为v2-v1;
在从队前返回队尾的过程中,通讯兵相对于队伍的速度为v2+v1.通讯兵两次相对于队伍的位移均为l,设运动的时间分别为t1、t2,
则有:t1=$\frac{L}{{v}_{2}-{v}_{1}}$,t2=$\frac{L}{{v}_{2}+{v}_{1}}$
通讯兵通过的路程为两段路程的和,即有:s=v2t1+v2t2
将上面的关系式代入得:s′=v2($\frac{L}{{v}_{2}-{v}_{1}}$+$\frac{L}{{v}_{2}+{v}_{1}}$)
整个个过程中,通讯兵通过的位移大小等于队伍前进的距离,即有:
x=v1($\frac{L}{{v}_{2}-{v}_{1}}$+$\frac{L}{{v}_{2}+{v}_{1}}$)
答:这个过程中通信兵通过的路程为v2($\frac{L}{{v}_{2}-{v}_{1}}$+$\frac{L}{{v}_{2}+{v}_{1}}$),位移x为v1($\frac{L}{{v}_{2}-{v}_{1}}$+$\frac{L}{{v}_{2}+{v}_{1}}$).
点评 本题考查位移和路程的计算,关键是计算向前的距离和向后的距离,难点是知道向前的时候人和队伍前进方向相同,向后的时候人和队伍前进方向相反

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
18.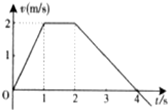 一个物体静止在粗糙的水平面上,受方向恒定的水平拉力作用,拉力的大小先后F1、F2、F3,物体在t=4s是停下,其v-t图象如图所示,已知物体与水平面间的动摩擦因数处处相同,下列判断正确的是( )
一个物体静止在粗糙的水平面上,受方向恒定的水平拉力作用,拉力的大小先后F1、F2、F3,物体在t=4s是停下,其v-t图象如图所示,已知物体与水平面间的动摩擦因数处处相同,下列判断正确的是( )
 一个物体静止在粗糙的水平面上,受方向恒定的水平拉力作用,拉力的大小先后F1、F2、F3,物体在t=4s是停下,其v-t图象如图所示,已知物体与水平面间的动摩擦因数处处相同,下列判断正确的是( )
一个物体静止在粗糙的水平面上,受方向恒定的水平拉力作用,拉力的大小先后F1、F2、F3,物体在t=4s是停下,其v-t图象如图所示,已知物体与水平面间的动摩擦因数处处相同,下列判断正确的是( )| A. | 0~1 s内的平均速度小于2~4s内的平均速度 | |
| B. | 0~2s内的平均速度大于1~4s内的平均速度 | |
| C. | 一定有F1+F3<2F2 | |
| D. | 一定有F1+F3>2F2 |
5.下列说法正确的是( )
| A. | 氢原子从激发态向基态跃迁只能辐射特定频率的光子 | |
| B. | 卢瑟福的α粒子散射实验揭示了原子核具有复杂的结构 | |
| C. | 采用物理或化学方法可以有效地改变放射性元素的半衰期 | |
| D. | 增加入射光的强度,不能增加光电子的动能 |
2. 如图所示,劲度系数为k的轻质弹簧下端固定在倾角为θ的粗糙斜面底端的挡板C上,另一端自然伸长到A点.质量为m的物块从斜面上B点由静止开始滑下,与弹簧发生相互作用,最终停在斜面上某点.下列说法正确的是( )
如图所示,劲度系数为k的轻质弹簧下端固定在倾角为θ的粗糙斜面底端的挡板C上,另一端自然伸长到A点.质量为m的物块从斜面上B点由静止开始滑下,与弹簧发生相互作用,最终停在斜面上某点.下列说法正确的是( )
 如图所示,劲度系数为k的轻质弹簧下端固定在倾角为θ的粗糙斜面底端的挡板C上,另一端自然伸长到A点.质量为m的物块从斜面上B点由静止开始滑下,与弹簧发生相互作用,最终停在斜面上某点.下列说法正确的是( )
如图所示,劲度系数为k的轻质弹簧下端固定在倾角为θ的粗糙斜面底端的挡板C上,另一端自然伸长到A点.质量为m的物块从斜面上B点由静止开始滑下,与弹簧发生相互作用,最终停在斜面上某点.下列说法正确的是( )| A. | 物块第一次滑到A点时速度最大 | |
| B. | 物块速度最大时弹簧的压缩量小于$\frac{mgsinθ}{k}$ | |
| C. | 物块压缩弹簧后被反弹过程做加速度逐渐减小的加速运动 | |
| D. | 物块最终停在斜面上时物块受到的摩擦力小于mgsinθ |
 如图所示,有一长度L=1m、质量M=10kg的平板小车静止在光滑的水平面上,在小车一端放置一质量m=4kg的小物块,物块与小车间的动摩擦因数μ=0.25,要使物块在2s内运动到小车的另一端,求:(g取10m/s2)
如图所示,有一长度L=1m、质量M=10kg的平板小车静止在光滑的水平面上,在小车一端放置一质量m=4kg的小物块,物块与小车间的动摩擦因数μ=0.25,要使物块在2s内运动到小车的另一端,求:(g取10m/s2) 
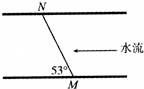 2015年7月17日,一年一度的“中国Cg高校建德新安江龙舟赛”在建德新安江上展开角逐.如图某龙舟队在比赛前划向比赛点的途中要渡过48m宽两岸平直的河,河中水流的速度均为v=5.0m/s.龙舟从M处开出后沿直线MN实际航行到达对岸,若直线MN与河岸成53°角,龙舟在静水中的速度大小也为5.0m/s,已知sin53°=0.8,cos53°=0.6,则龙舟从M点沿直线MN到达对岸所经历的时间为( )
2015年7月17日,一年一度的“中国Cg高校建德新安江龙舟赛”在建德新安江上展开角逐.如图某龙舟队在比赛前划向比赛点的途中要渡过48m宽两岸平直的河,河中水流的速度均为v=5.0m/s.龙舟从M处开出后沿直线MN实际航行到达对岸,若直线MN与河岸成53°角,龙舟在静水中的速度大小也为5.0m/s,已知sin53°=0.8,cos53°=0.6,则龙舟从M点沿直线MN到达对岸所经历的时间为( )