题目内容
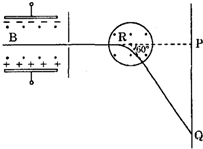如图所示，相距为d的两平行金属板内存在垂直纸面向外的匀强磁场，磁感应强度为B，调节两极板间电压使沿中线入射的正离子能做直线运动打到荧光屏上的P点，此时两极板间电压为U．另加一半径为R的圆形磁场，使正离子偏转60°角，打到荧光屏上的Q点，求此正离子在圆形磁场中所经历的时间．分析：正离子能做直线运动，说明电场力与洛伦兹力平衡，据此求出运动速度，设粒子在磁场中运动轨道半径为r，圆形磁场磁感应强度为B′；
根据几何关系求出圆周运动的半径，根据洛伦兹力提供向心力公式及周期公式联立方程即可求解．
根据几何关系求出圆周运动的半径，根据洛伦兹力提供向心力公式及周期公式联立方程即可求解．
解答：解：设飞出速度选择器的离子速度为v，
q
=qvB
解得：v=
①
设粒子在磁场中运动轨道半径为r，圆形磁场磁感应强度为B′，
r=Rcot30°=
R②
洛伦兹力提供向心力，则：qvB′=m
解得：r=
③
正离子在磁场中经历的时间t=
T=
T=
?
④
由①②③④解得：t=
答：正离子在圆形磁场中所经历的时间为
．
q
| U |
| d |
解得：v=
| U |
| Bd |
设粒子在磁场中运动轨道半径为r，圆形磁场磁感应强度为B′，
r=Rcot30°=
| 3 |
洛伦兹力提供向心力，则：qvB′=m
| v2 |
| r |
解得：r=
| mv |
| B′q |
正离子在磁场中经历的时间t=
| 60° |
| 360° |
| 1 |
| 6 |
| 1 |
| 6 |
| 2πm |
| qB′ |
由①②③④解得：t=
| ||
| 3U |
答：正离子在圆形磁场中所经历的时间为
| ||
| 3U |
点评：本题中离子先在速度选择器中做匀速直线运动、在磁场中做匀速圆周运动，磁场中画出轨迹，找出半径是解题的关键，根据平衡条件、向心力公式及周期公式即可处理这类问题．
练习册系列答案
相关题目
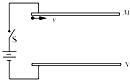如图所示，相距为d的两块平行金属板M、N与电源相连接．当开关S闭合后，一个重力可以忽略不计的带电粒子，垂直于电场方向从M板的边缘射入电场，恰好打在N板的中央．如果保持开关S闭合，欲使该粒子能刚好从下极板边缘飞出电场，则N板应向下平移多少？
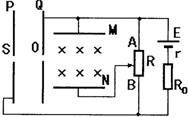（2003?顺德区模拟）如图所示，相距为d的水平金属板M、N在左侧有一对竖直金属板P、Q，板P上的小孔S正对极Q上的小孔O，M、N间有垂直纸面向里的匀强磁场，在小孔S处有一带负电粒子，其重力和初速均不计，当变阻器的滑动触头在AB的中点时，带负电粒子恰能在M、N间做直线运动，当滑动变阻器滑片滑到A点后，（ ）
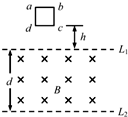（2013?静安区二模）如图所示，相距为d的两条水平虚线L1、L2之间有水平方向的匀强磁场，磁感应强度为B，正方形铜制线圈abcd边长为L（L＜d），质量为m，将线圈在磁场上方高h处静止释放，cd边刚离开磁场时速度与cd边刚进入磁场时速度相等，则线圈穿越磁场的过程中（从cd边刚进入磁场起一直到ab边离开磁场为止），感应电流所做的功为
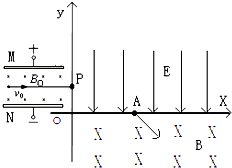如图所示，相距为d的平行金属板M、N间存在匀强电场和垂直纸面向里、磁感应强度为Bo的匀强磁场；在xoy直角坐标平面内，第一象限有沿y轴负方向场强为E的匀强电场，第四象限有垂直坐标平面向里、磁感应强度为B的匀强磁场．一质量为m、电量为q的正离子（不计重力）以初速度Vo沿平行于金属板方向射入两板间并做匀速直线运动．从P点垂直y轴进入第一象限，经过x轴上的A点射出电场，进入磁场．已知离子过A点时的速度方向与x轴成45°角．求：