题目内容
7.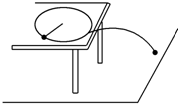 如图所示,一根长0.1m的细线,一端系着一个质量为0.18kg的小球,拉住线的另一端,使小球在光滑的水平桌面上做匀速圆周运动.如果小球的转速缓慢地增加到开始时转速的3倍时细线断开,细线断开前的瞬间受到的拉力比开始时大40N,求:
如图所示,一根长0.1m的细线,一端系着一个质量为0.18kg的小球,拉住线的另一端,使小球在光滑的水平桌面上做匀速圆周运动.如果小球的转速缓慢地增加到开始时转速的3倍时细线断开,细线断开前的瞬间受到的拉力比开始时大40N,求:(1)细线断开前的瞬间小球受到的拉力大小;
(2)线断开的瞬间,小球运动的线速度大小;
(3)如果小球离开桌面时,速度方向恰好与桌面边线垂直,桌面高出地面0.8m,求:小球飞出后的落地点距桌边线的水平距离.
分析 (1)线末断开前,由线的拉力提供向心力.由题意:小球的转速增加到开始时转速的3倍时细线断开,根据向心力公式可得到线断开时线的拉力与原来拉力的倍数;结合条件:线断开前的瞬间线的拉力比开始时大40N,即可求出线断开前的瞬间,线的拉力大小.
(2)由向心力公式F=m$\frac{{v}^{2}}{R}$求出小球的速度大小.
(3)小球离开桌面后做平抛运动,由高度求出时间,并求出平抛运动的水平位移,根据所求的距离与水平位移的数学关系求解.
解答 解:(1)线的拉力等于向心力,设开始时角速度为ω0,向心力是F0,线断开的瞬间,角速度为ω,线的拉力是F.
则有:${F}_{0}=m{{ω}_{0}}^{2}R$…①
F=mω2R…②
由①②得:$\frac{F}{{F}_{0}}=\frac{9}{1}$…③
又因为F=F0+40N…④
由③④得:F=45N
(2)设线断开时速度为v
由$F=m\frac{{v}^{2}}{R}$,
得:v=$\sqrt{\frac{FR}{m}}$=5m/s
(3)设桌面高度为h,小球落地经历时间为t.
根据h=$\frac{1}{2}g{t}^{2}$
得:t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×0.8}{10}}=0.4s$
小球飞出后的落地点距桌边线的水平距离x=vt=5×0.4=2m
答:(1)细线断开前的瞬间小球受到的拉力大小为45N;
(2)线断开的瞬间,小球运动的线速度大小为5m/s;
(3)小球飞出后的落地点距桌边线的水平距离为2m.
点评 对于匀速圆周运动,基本方程是“指向圆心的合力”等于向心力,即F合=Fn,关键分析向心力的来源,知道小球离开桌面后做平抛运动,难度适中.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
17.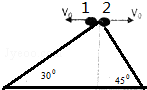 两个同高度斜面,倾角分别为30°、45°,小球1、2分别由斜面顶端以相等水平速度抛出,如图所示,假设两球能落在斜面上,则小球1、2飞行下落的时间之比为( )
两个同高度斜面,倾角分别为30°、45°,小球1、2分别由斜面顶端以相等水平速度抛出,如图所示,假设两球能落在斜面上,则小球1、2飞行下落的时间之比为( )
 两个同高度斜面,倾角分别为30°、45°,小球1、2分别由斜面顶端以相等水平速度抛出,如图所示,假设两球能落在斜面上,则小球1、2飞行下落的时间之比为( )
两个同高度斜面,倾角分别为30°、45°,小球1、2分别由斜面顶端以相等水平速度抛出,如图所示,假设两球能落在斜面上,则小球1、2飞行下落的时间之比为( )| A. | 1:1 | B. | $\sqrt{3}$:3 | C. | 3:$\sqrt{3}$ | D. | 3:1 |
18.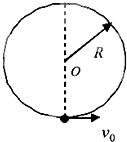 如图所示,半径为R的金属环竖直放置,环上套有一质量为m的小球,小球开始时静止于最低点.现给小球一冲击,使它以初速度v0=$\sqrt{6gR}$.小球运动到环的最高点时与环恰无作用力,小球从最低点运动到最高点的过程中( )
如图所示,半径为R的金属环竖直放置,环上套有一质量为m的小球,小球开始时静止于最低点.现给小球一冲击,使它以初速度v0=$\sqrt{6gR}$.小球运动到环的最高点时与环恰无作用力,小球从最低点运动到最高点的过程中( )
 如图所示,半径为R的金属环竖直放置,环上套有一质量为m的小球,小球开始时静止于最低点.现给小球一冲击,使它以初速度v0=$\sqrt{6gR}$.小球运动到环的最高点时与环恰无作用力,小球从最低点运动到最高点的过程中( )
如图所示,半径为R的金属环竖直放置,环上套有一质量为m的小球,小球开始时静止于最低点.现给小球一冲击,使它以初速度v0=$\sqrt{6gR}$.小球运动到环的最高点时与环恰无作用力,小球从最低点运动到最高点的过程中( )| A. | 小球机械能守恒 | |
| B. | 小球在最低点时对金属环的压力是6mg | |
| C. | 小球在最高点时,重力的功率是mg=$\sqrt{gR}$ | |
| D. | 小球机械能不守恒,且克服摩擦力所做的功是0 5mgR |
2.以下说法正确的是( )
| A. | 哥白尼提出了“地心说” | |
| B. | 被命名为“笔尖下发现的行星”是天王星 | |
| C. | 卡文迪许在利用扭秤实验装置测量万有引力常量时,应用了“放大法” | |
| D. | 经典力学适用于宏观物体的运动,量子力学适用于微观粒子的运动 |
12.关于内能,下列说法正确的是( )
| A. | 由于水结成冰后体积增大,所以冰的内能大于水的内能 | |
| B. | 1kg 0℃的水的内能大于1kg 0℃的冰的内能 | |
| C. | 同体积的物体,质量大的内能一定大 | |
| D. | 同质量的物体,体积大的内能一定大 |
19.质量为5m的机车以速度v运动,此时分别跟质量都为m的3节静止车厢挂接,挂接在一起时的速度为( )
| A. | $\frac{v}{3}$ | B. | $\frac{v}{5}$ | C. | $\frac{5v}{8}$ | D. | $\frac{v}{8}$ |
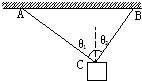 如图所示,重为G的物体在两根细绳的悬挂下处于静止状态,细绳AC、BC与竖直方向的夹角分别为θ1=60°,θ2=30°,求细绳AC、BC对物体的拉力F1、F2各为多大?
如图所示,重为G的物体在两根细绳的悬挂下处于静止状态,细绳AC、BC与竖直方向的夹角分别为θ1=60°,θ2=30°,求细绳AC、BC对物体的拉力F1、F2各为多大? 如图所示,有一质量为0.5kg的小球,用绳子系住小球在竖直平面内做圆周运动,转动半径为0.5m,小球通过最高点的速度为4m/s,不计空气阻力,g取10m/s2,
如图所示,有一质量为0.5kg的小球,用绳子系住小球在竖直平面内做圆周运动,转动半径为0.5m,小球通过最高点的速度为4m/s,不计空气阻力,g取10m/s2,