题目内容
【题目】如图所示，有一内壁光滑的闭合椭圆形管道，置于竖直平面内，MN是通过椭圆中心O点的水平线．已知一小球从M点出发，初速率为v0，沿管道MPN运动，到N点的速率为v1，所需时间为t1；若该小球仍由M点以初速率v0出发，而沿管道MQN运动，到N点的速率为v2，所需时间为t2，则（ ）
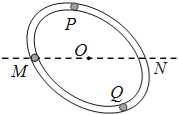
A. v1=v2，t1＞t2 B. v1＜v2，t1＞t2 C. v1=v2，t1＜t2 D. v1＜v2，t1＜t2
【答案】A
【解析】试题分析：根据机械能守恒定律分析小球到达N点时速率关系，结合小球的运动情况，分析平均速率关系，即可得到结论．
解：由于小球在运动过程中只有重力做功，机械能守恒，到达N点时速率相等，即有v1=v2．
小球沿管道MPN运动时，根据机械能守恒定律可知在运动过程中小球的速率小于初速率v0，而小球沿管道MQN运动，小球的速率大于初速率v0，所以小球沿管道MPN运动的平均速率小于沿管道MQN运动的平均速率，而两个过程的路程相等，所以有t1＞t2．故A正确．
故选：A
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
