题目内容
2013年12月15日“嫦娥三号”探测器成功实现“月面软着陆”.若着陆的最后阶段可简化为三个过程:①探测器从月球表面附近高为H处开始匀减速竖直下降至静止;②悬停(即处于静止状态);③自由下落至月球表面.为了保证探测器的安全,要求探测器到达月球表面的速度不能超过vm,月球表面附近的重力加速度为g0,探测器在减速过程中每秒钟消耗的燃料为△m=pa+q(a为探测器匀减速下降的加速度大小,p、q为大于零的常数).忽略探测器因消耗燃料而引起的质量变化.
(1)求探测器悬停位置距月球表面的最大高度hm;
(2)若在(1)中悬停最大高度hm不变的情况下,为使探测器减速下降过程中消耗的燃料质量最少,则该过程中探测器的加速度为多大,最低消耗燃料的质量m为多少.
(1)求探测器悬停位置距月球表面的最大高度hm;
(2)若在(1)中悬停最大高度hm不变的情况下,为使探测器减速下降过程中消耗的燃料质量最少,则该过程中探测器的加速度为多大,最低消耗燃料的质量m为多少.
(1)在自由下落到月球表面的过程中,由vm2=2g0hm
解得:hm=
(2)探测器从高为H处匀减速下降到hm悬停位置的过程中,由运动学公式得:
H-hm=
at2;
又m=△m△t=(ap+q)
=(p
+
)
由上式可知,当p
=
时
即a=
时,所消耗的燃料最少
则有:m=2
×
=2
)
答:(1)探测器悬停位置距月球表面的最大高度hm为
;
(2)最低消耗燃料的质量m为2
)..
解得:hm=
| ||
| 2g0 |
(2)探测器从高为H处匀减速下降到hm悬停位置的过程中,由运动学公式得:
H-hm=
| 1 |
| 2 |
又m=△m△t=(ap+q)
|
| a |
| q | ||
|
| 2(H-hm) |
由上式可知,当p
| a |
| q | ||
|
即a=
| q |
| p |
则有:m=2
| pq |
| 2(H-hm) |
pq(H-
|
答:(1)探测器悬停位置距月球表面的最大高度hm为
| ||
| 2g0 |
(2)最低消耗燃料的质量m为2
pq(H-
|

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目

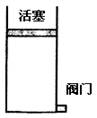
 的冰水混合物中气体达到平衡状态
的冰水混合物中气体达到平衡状态 ,测得气体的体积为
,测得气体的体积为 ,然后将气缸从冰水混合物中移出后,在室温(
,然后将气缸从冰水混合物中移出后,在室温( )中达到平衡状态
)中达到平衡状态 ,外界大气压强保持不变.求:
,外界大气压强保持不变.求:
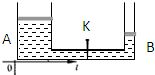
 时,管内用水银封闭着长L1=8cm的空气柱,这时两管内水银面等高,已知大气压强为
时,管内用水银封闭着长L1=8cm的空气柱,这时两管内水银面等高,已知大气压强为 cmHg。
cmHg。
