题目内容
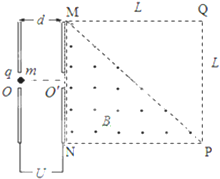 如图所示,长度均为L的两平行金属板相距为d,O、O′为两金属板中心处正对的两个小孔,两平行金属板接有电压恒为U的电源.紧靠右金属板右侧的边长为L的正方形MQPN的左下半空间有匀强磁场,MN与右金属板重合.一质量为m、带电量为-q的带负电粒子(重力不计)从O点以可忽略的初速度进入金属板间的电场,经加速后再进入磁场区,恰好垂直MP而离开磁场区.试求:
如图所示,长度均为L的两平行金属板相距为d,O、O′为两金属板中心处正对的两个小孔,两平行金属板接有电压恒为U的电源.紧靠右金属板右侧的边长为L的正方形MQPN的左下半空间有匀强磁场,MN与右金属板重合.一质量为m、带电量为-q的带负电粒子(重力不计)从O点以可忽略的初速度进入金属板间的电场,经加速后再进入磁场区,恰好垂直MP而离开磁场区.试求:(1)磁感应强度B的大小;
(2)带电粒子从O点进入电场到最后从MP离开磁场的时间t.
分析:(1)带电粒子先经电场加速,后进入磁场偏转.根据几何关系得到磁场中轨迹半径,由牛顿第二定律求出B的大小.
(2)分两段求时间:微粒在电场中做匀加速直线运动,由运动学公式求时间;磁场中,根据轨迹对应的圆心角θ,由t=
T求时间或由t=
,s是弧长.
(2)分两段求时间:微粒在电场中做匀加速直线运动,由运动学公式求时间;磁场中,根据轨迹对应的圆心角θ,由t=
| θ |
| 2π |
| s |
| v |
解答:解:(1)在电场中,由动能定理得:
qU=
mv2-0…①
得:v=
…②
在磁场中,微粒做匀速圆周运动,由几何知识得知,轨迹半径为:R=
…③
由qvB=m
…④
可解得:B=
…⑤
(2)在电场中,运动时间为:t1=
…⑥
在磁场中,运动时间为:t2=
…⑦
联立②⑥⑦得:t=t1+t2=(2d+
)
答:
(1)磁感应强度B的大小是
;
(2)带电粒子从O点进入电场到最后从MP离开磁场的时间t是(2d+
)
.
qU=
| 1 |
| 2 |
得:v=
|
在磁场中,微粒做匀速圆周运动,由几何知识得知,轨迹半径为:R=
| L |
| 2 |
由qvB=m
| v2 |
| R |
可解得:B=
| 2 |
| L |
|
(2)在电场中,运动时间为:t1=
| d | ||
|
在磁场中,运动时间为:t2=
| ||
| v |
联立②⑥⑦得:t=t1+t2=(2d+
| πL |
| 8 |
|
答:
(1)磁感应强度B的大小是
| 2 |
| L |
|
(2)带电粒子从O点进入电场到最后从MP离开磁场的时间t是(2d+
| πL |
| 8 |
|
点评:本题主要考查了带电粒子在组合场中运动的问题,要能正确分析粒子的受力情况,画出运动轨迹,由几何知识求半径是解题的关键.根据圆心角求解粒子在磁场中运动的时间.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
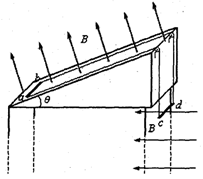
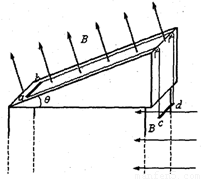
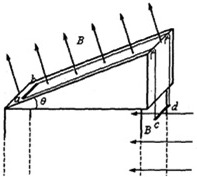 如图所示,长度均为l、电阻均为R的两导体杆ab、cd,通过两条足够长的不可伸缩的轻质柔软导线连接起来(导线电阻不计),形成闭合回路,并分别跨过两个间距为l的定滑轮,使ab水平置于倾角为θ的足够长绝缘斜面上,cd水平悬挂于竖直平面内.斜面上的空间内存在垂直斜面向上的磁感应强度为B的匀强磁场,cd杆初始位置以下的空间存在水平向左的磁感应强度也为B的匀强磁场.ab、cd杆质量均为m,ab杆与斜面间的动摩擦因数为μ,不计滑轮的一切阻力.
如图所示,长度均为l、电阻均为R的两导体杆ab、cd,通过两条足够长的不可伸缩的轻质柔软导线连接起来(导线电阻不计),形成闭合回路,并分别跨过两个间距为l的定滑轮,使ab水平置于倾角为θ的足够长绝缘斜面上,cd水平悬挂于竖直平面内.斜面上的空间内存在垂直斜面向上的磁感应强度为B的匀强磁场,cd杆初始位置以下的空间存在水平向左的磁感应强度也为B的匀强磁场.ab、cd杆质量均为m,ab杆与斜面间的动摩擦因数为μ,不计滑轮的一切阻力.