题目内容
黑洞是爱因斯坦的广义相对论中预言的一种特殊天体，它的密度极大，对周围的物质有极强的吸引力，根据恩爱斯坦理论，光子是有质量的，光子到达黑洞表面时也将被吸入，最多恰能绕黑洞表面做匀速圆周运动，根据天文观测，银河系中心可能有一个黑洞，距该黑洞6.0×1012m远的星体正以2.0×106m/s的速度绕它旋转，距此估算可能黑洞的最大半径为多大？（保留一位有效数字）
分析：根据距该黑洞6.0×1012m远的星体正以2.0×106m/s的速度绕它旋转，写出万有引力提供向心力的公式，求得黑洞的质量；光子到达黑洞表面最多恰能绕黑洞表面做匀速圆周运动，写出万有引力提供向心力的公式，求得黑洞的最大半径．
解答：解：对围绕黑洞做圆周运动的星体应用牛顿第二定律得
=
即 GM=v2r
由黑洞特点可知，光子到达黑洞表面最多恰能绕黑洞表面做匀速圆周运动，对光子应用牛顿第二定律，得
≥
即 R=
所以 R=
=
≈3×108
答：黑洞的最大半径为3×108m
| GMm |
| r2 |
| mv2 |
| r |
即 GM=v2r
由黑洞特点可知，光子到达黑洞表面最多恰能绕黑洞表面做匀速圆周运动，对光子应用牛顿第二定律，得
| GMmc |
| R2 |
| mcc2 |
| R |
即 R=
| GM |
| c2 |
所以 R=
| v2r |
| c2 |
| (2.0×106)2×6.0×1012 |
| (3.0×108)2 |
答：黑洞的最大半径为3×108m
点评：该题结合黑洞的物理现象考查万有引力定律的应用，有较好的创新型，是一道理论联系实际的好题．
练习册系列答案
相关题目
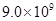km处有一颗恒星以200km／s的速度绕其旋转。根据以上信息，试估算这一“黑洞”的半径R=_____m。（已知c=3×105km／s保留一位有效数字）