题目内容
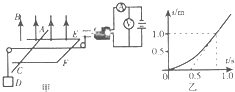 如图甲所示,光滑导体框架水平放置,空间有竖直向上的匀强磁场,磁感应强度为B=1T,质量为m=0.1kg、电阻为R=4Ω的导体棒AC横放在框架上.现用轻绳栓住导体棒,轻绳的一端通过光滑的定滑轮绕在电动机的转轴上,另一端通过光滑的定滑轮与质量为M=0.3kg的物体D相连,电动机的内阻为R=1Ω.电路接通后,导体棒AC平行于EF向右运动(其运动情况如图乙所示),且电压表的读数恒为U=8V,电流表的读数恒为I=1A.不计导体框的电阻,g=10m/s2,求:
如图甲所示,光滑导体框架水平放置,空间有竖直向上的匀强磁场,磁感应强度为B=1T,质量为m=0.1kg、电阻为R=4Ω的导体棒AC横放在框架上.现用轻绳栓住导体棒,轻绳的一端通过光滑的定滑轮绕在电动机的转轴上,另一端通过光滑的定滑轮与质量为M=0.3kg的物体D相连,电动机的内阻为R=1Ω.电路接通后,导体棒AC平行于EF向右运动(其运动情况如图乙所示),且电压表的读数恒为U=8V,电流表的读数恒为I=1A.不计导体框的电阻,g=10m/s2,求:(1)电动机的输出功率;
(2)匀强磁场的宽度;
(3)导体棒在变速阶段产生的热量.
分析:(1)电动机的输出功率等于输入功率与内电路发热功率之差.电动机的输入功率为 P1=UI,输出功率为 P2=P1-I2r.
(2)导体棒最终做匀速直线运动,合外力为零,根据E=BLv,电流I=
,安培力F安=BIL得到安培力与速度v的关系,根据图象的斜率求出匀速运动的速度,再根据平衡条件求解匀强磁场的宽度.
(3)根据能量守恒定律列方程,求解导体棒在变速阶段产生的热量.
(2)导体棒最终做匀速直线运动,合外力为零,根据E=BLv,电流I=
| E |
| R |
(3)根据能量守恒定律列方程,求解导体棒在变速阶段产生的热量.
解答:解:(1)电动机的输入功率 P1=UI=8W
电动机的输出功率 P2=P1-I2r=7W
(2)导体棒最终做匀速直线运动,设速度为v,此时棒的电动势为E=BLv
电流 I=
安培力F安=BIL
设右端线的拉力为F,由平衡条件得:F=Mg+F安
由图象知,棒匀速运动的速度为 v=
=
=2m/s
又 P2=Fv
由以上各式解得:L=1m
(3)对系统由能量守恒得:
P2t=
(m+M)v2+Mgs+Q
其中t=1s,s=1m
代入数据解得:Q=3.2J
答:(1)电动机的输出功率为7W;(2)匀强磁场的宽度为1m;(3)导体棒在变速阶段产生的热量为3.2J.
电动机的输出功率 P2=P1-I2r=7W
(2)导体棒最终做匀速直线运动,设速度为v,此时棒的电动势为E=BLv
电流 I=
| E |
| R |
安培力F安=BIL
设右端线的拉力为F,由平衡条件得:F=Mg+F安
由图象知,棒匀速运动的速度为 v=
| △s |
| △t |
| 1 |
| 0.5 |
又 P2=Fv
由以上各式解得:L=1m
(3)对系统由能量守恒得:
P2t=
| 1 |
| 2 |
其中t=1s,s=1m
代入数据解得:Q=3.2J
答:(1)电动机的输出功率为7W;(2)匀强磁场的宽度为1m;(3)导体棒在变速阶段产生的热量为3.2J.
点评:考查图象的斜率表示的含义,掌握总功率与各消耗功率的关系,理解能量守恒定律在本题的应用.注意安培力做功与产生热量的相对应,不能重复.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目



