题目内容
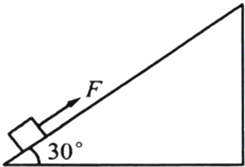 倾角为30°的足够长的光滑斜面上有一质量为2kg的物块,在t=0时刻给物块施加一个平行于斜面向上、大小为20N的恒定外力F,物块由静止开始沿斜面向上运动,在第3s末将20N的外力撤掉,则从物块开始运动至到达斜面最高点的过程中,下列说法正确的是(g取10 m/s2 )
倾角为30°的足够长的光滑斜面上有一质量为2kg的物块,在t=0时刻给物块施加一个平行于斜面向上、大小为20N的恒定外力F,物块由静止开始沿斜面向上运动,在第3s末将20N的外力撤掉,则从物块开始运动至到达斜面最高点的过程中,下列说法正确的是(g取10 m/s2 )分析:对物体进行受力分析,根据牛顿第二定律求出撤去外力前后物块的加速度,根据运动学基本公式判断时间和位移是否相等,运动到最高点时速度为零,根据动能定理判断整个过程外力F所做的功和物块克服重力所做的功的关系.
解答:解:A、物体受到恒定外力作用时,根据牛顿第二定律有:
F-mgsinθ=ma1
解得:a1=
=5m/s2
撤去F时的速度v=a1t1=15m/s
撤去F前位移为x1=
a1t12=
×5×9m=22.5m
撤去外力F后.有:
mgsinθ=ma2
解得:a2=gsinθ=10×0.5=5m/s2
运动到最高点时速度为零,则
t2=
=3s
位移x2=
=
=22.5m
从而可知,撤去外力前后物块运动的时间、位移、加速度相等,故ABC正确;
D、物体初末位置速度都为零,
根据动能定理得:整个过程中外力F做的功等于物块克服重力做的功,故D错误;
故选ABC
F-mgsinθ=ma1
解得:a1=
| 20-20×0.5 |
| 2 |
撤去F时的速度v=a1t1=15m/s
撤去F前位移为x1=
| 1 |
| 2 |
| 1 |
| 2 |
撤去外力F后.有:
mgsinθ=ma2
解得:a2=gsinθ=10×0.5=5m/s2
运动到最高点时速度为零,则
t2=
| v |
| a2 |
位移x2=
| v2 |
| 2a2 |
| 225 |
| 10 |
从而可知,撤去外力前后物块运动的时间、位移、加速度相等,故ABC正确;
D、物体初末位置速度都为零,
根据动能定理得:整个过程中外力F做的功等于物块克服重力做的功,故D错误;
故选ABC
点评:本题主要考查了牛顿第二定律、运动学基本公式、动能定理的直接应用,要求同学们能正确分析物体的运动情况,难度适中.

练习册系列答案
相关题目
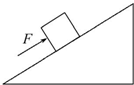 在倾角为30°的足够长的斜面上,有一重10N的物体,被平行于斜面的大小为8N的恒力F推着沿斜面匀速上滑,如图所示,g取10m/s2.物体所受最大静摩擦力与滑动摩擦力相等.在推力F突然消失的瞬间( )
在倾角为30°的足够长的斜面上,有一重10N的物体,被平行于斜面的大小为8N的恒力F推着沿斜面匀速上滑,如图所示,g取10m/s2.物体所受最大静摩擦力与滑动摩擦力相等.在推力F突然消失的瞬间( )| A、物体所受摩擦力方向立即与原来相反 | B、物体的瞬时加速度为8m/s2 | C、物体与斜面间的动摩擦因数等于0.4 | D、推力F消失后,物体将沿斜面上滑,最后静止在斜面上 |
 如图所示,倾角为θ=30°的足够长的固定斜面上,在底端0处固定一垂直斜面的档板,斜面上OM段光滑,M点及以上均粗糙.质量为m的物块A在M点恰好能静止,有一质量为2m的光滑小物块B以初速度
如图所示,倾角为θ=30°的足够长的固定斜面上,在底端0处固定一垂直斜面的档板,斜面上OM段光滑,M点及以上均粗糙.质量为m的物块A在M点恰好能静止,有一质量为2m的光滑小物块B以初速度 如图甲所示,倾角为30°的足够长的光滑斜面上,有一质量m=0.8kg的物体受到平行斜面向上的力F作用,其大小F随时间t变化的规律如图乙所示,t=0时刻物体在斜面上的中点且速度为零,重力加速度g=10m/s2.下列说法中不正确的是( )
如图甲所示,倾角为30°的足够长的光滑斜面上,有一质量m=0.8kg的物体受到平行斜面向上的力F作用,其大小F随时间t变化的规律如图乙所示,t=0时刻物体在斜面上的中点且速度为零,重力加速度g=10m/s2.下列说法中不正确的是( )
