Question

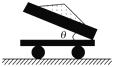
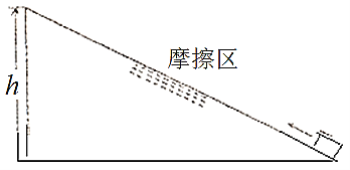
【题目】如图所示，一个物块以某一初速度沿倾角、高的固定光滑斜面的最下端向上远动，物块运动到斜面的顶端时的速率为，如果在斜面中间某一区域设置一段摩擦区，物块与摩擦区之间的动摩擦因数，物块以同样的初速度从斜面的底端向上运动，物块恰好运动到斜面的项端（，，，）。

(1)求初速度的大小；

(2)求摩擦区的长度；

(3)在设置摩擦区后，摩擦区的位置不同，物块以初速度从斜面底端运动到斜面顶端的时间不同，求物块从斜面底端运动到斜面顶端的最长时间（计算结果保留两位小数）。

Answer 1

【答案】（1）6m/s（2）1m（3）0.97s

【解析】(1)由动能定理得到：

代入已知数据可以得到：

(2)增设摩擦区后，因物块恰好运动到斜面的顶端，则摩擦力做功恰好等于没有摩擦区域时物块运动到斜面顶端的动能，则：，

代入数据可以得到：；

(3)如图所示，当摩擦区设置在斜面最小面时，让物块一开始运动就进入摩擦区，物块在斜面上运动的时间最长，设物块在摩擦区和光滑的斜面上的加速度分别是a1和a2，则：

，

代入数据可以得到：，

物块在摩擦区内运动的时间为t1，则：，

代入数据得到：

物块在斜面的光滑部分运动的初速度为，时间为，

则：，

物块运动到斜面顶端的最长时间为：。