题目内容
将一物体竖直上抛,若物体所受空气阻力与其运动速度成正比,以竖直向上为正方向,则抛出后物体的速度随时间变化的图象可能是下列图中的( )
A、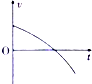 | B、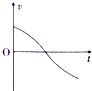 | C、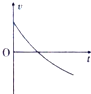 | D、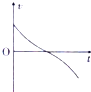 |
分析:根据阻力和速度的关系,利用牛顿第二定律得出加速度的表达式,结合速度时间图线的切线斜率表示加速度得出正确的速度随时间图线.
解答:解:由题知:物体受到阻力:f=kv
当物体向上运动时,根据牛顿第二定律得:a=
由于v减小则a减小,结合图象的斜率表示加速度的大小,故A、B错误;
当物体向下运动时,由牛顿第二定律得:a=
由于v增大则a减小,结合图象的斜率表示加速度的大小,故C正确,D错误.
故选:C.
当物体向上运动时,根据牛顿第二定律得:a=
| mg+f |
| m |
由于v减小则a减小,结合图象的斜率表示加速度的大小,故A、B错误;
当物体向下运动时,由牛顿第二定律得:a=
| mg-kv |
| m |
由于v增大则a减小,结合图象的斜率表示加速度的大小,故C正确,D错误.
故选:C.
点评:解决本题的关键知道速度时间图线的切线斜率表示加速度,利用牛顿第二定律表示加速度的表达式判断选项.

练习册系列答案
相关题目
 ,试求:
,试求: