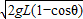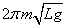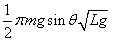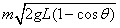题目内容
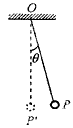
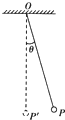 如图所示,一单摆摆长为L,摆球质量为m,悬挂于O点.现将小球拉至P点,然后释放,使小球做简谐运动,小球偏离竖直方向的最大角度为θ.已知重力加速度为g.在小球由P点运动到最低点P′的过程中,求:
如图所示,一单摆摆长为L,摆球质量为m,悬挂于O点.现将小球拉至P点,然后释放,使小球做简谐运动,小球偏离竖直方向的最大角度为θ.已知重力加速度为g.在小球由P点运动到最低点P′的过程中,求:(1)小球所受合力的冲量;
(2)小球所受重力的冲量;
(3)小球所受拉力冲量的大小.
分析:(1)由动能定理求出到达P′的速度,由动量定理,合外力的冲量等于物体动量的改变量.
(2)根据周期公式求出小球运动的时间,根据I=Ft求解重力的冲量.
(3)根据平行四边形定则求解拉力的冲量.
(2)根据周期公式求出小球运动的时间,根据I=Ft求解重力的冲量.
(3)根据平行四边形定则求解拉力的冲量.
解答:解:(1)在小球由P点运动到最低点P′的过程中,根据动能定理,有:
mgL(1-cosθ)=
mv2
解得:v=m
根据动量定理,合力的冲量为:
I合=mv=m
;方向水平向左;
(2)单摆的摆动周期为:T=2π
;
小球由P点运动到最低点P′的为:t=0.25T=
π
故重力的冲量为:IG=mg
=
πm
;方向竖直向下;
(3)合力的冲量等于重力的冲量与拉力的冲量,矢量图如下:
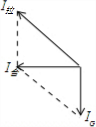
故拉力的冲量为:I拉=
=m
;
答:(1)小球所受合力的冲量为m
,方向水平向左;
(2)小球所受重力的冲量为
πm
,方向竖直向下;
(3)小球所受拉力冲量的大小为m
.
mgL(1-cosθ)=
| 1 |
| 2 |
解得:v=m
| 2gL(1-cosθ) |
根据动量定理,合力的冲量为:
I合=mv=m
| 2gL(1-cosθ) |
(2)单摆的摆动周期为:T=2π
|
小球由P点运动到最低点P′的为:t=0.25T=
| 1 |
| 2 |
|
故重力的冲量为:IG=mg
| T |
| 4 |
| 1 |
| 2 |
| gL |
(3)合力的冲量等于重力的冲量与拉力的冲量,矢量图如下:

故拉力的冲量为:I拉=
| I合2+IG2 |
gL(2-2cosθ+
|
答:(1)小球所受合力的冲量为m
| 2gL(1-cosθ) |
(2)小球所受重力的冲量为
| 1 |
| 2 |
| gL |
(3)小球所受拉力冲量的大小为m
gL(2-2cosθ+
|
点评:本题主要考查了动量定理、简谐运动的周期公式及动能定理的直接应用,难度适中.

练习册系列答案
相关题目
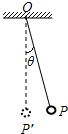 如图所示,一单摆摆长为L,摆球质量为m,悬挂于O点.现将小球拉至P点,然后释放,使小球做简谐运动,小球偏离竖直方向的最大角度为θ.已知重力加速度为g.在小球由P点运动到最低点P′的过程中( )
如图所示,一单摆摆长为L,摆球质量为m,悬挂于O点.现将小球拉至P点,然后释放,使小球做简谐运动,小球偏离竖直方向的最大角度为θ.已知重力加速度为g.在小球由P点运动到最低点P′的过程中( )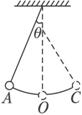

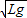
 πmgsinθ
πmgsinθ