题目内容
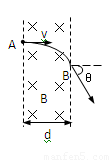
如图所示，一束电荷量为e的电子以垂直于磁感应强度B并垂直于磁场边界的速度v射入宽度为d的匀强磁场中，穿出磁场时速度方向和原来射入方向的夹角为θ=60°，求电子的质量和穿越磁场的时间．分析：作出粒子运动的轨迹图，结合几何关系求出电子在磁场中的半径，根据洛伦兹力提供向心力求出电子的质量．根据几何关系求出电子在磁场中的圆心角，结合周期公式求出穿越磁场的时间．
解答：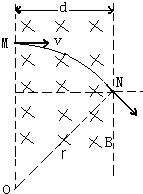
解：粒子的运动轨迹图如图所示，根据几何关系有：r=
=
d
根据洛伦兹力提供向心力得，Bev=m
解得电子的质量m=
电子的周期T=
=
所以电子穿越磁场的时间t=
T=
．
答：电子的质量为m=
，穿越磁场的时间为t=
．
解：粒子的运动轨迹图如图所示，根据几何关系有：r=| d |
| sin60° |
2
| ||
| 3 |
根据洛伦兹力提供向心力得，Bev=m
| v2 |
| r |
解得电子的质量m=
2
| ||
| 3v |
电子的周期T=
| 2πr |
| v |
4
| ||
| 3v |
所以电子穿越磁场的时间t=
| 1 |
| 6 |
2
| ||
| 9v |
答：电子的质量为m=
2
| ||
| 3v |
2
| ||
| 9v |
点评：解决本题的关键作出电子的运动轨迹图，结合几何关系，运用半径公式和周期公式进行求解．
练习册系列答案
相关题目
（2013?浙江）“电子能量分析器”主要由处于真空中的电子偏转器和探测板组成．偏转器是由两个相互绝缘、半径分别为RA和RB的同心金属半球面A和B构成，A、B为电势值不等的等势面，其过球心的截面如图所示．一束电荷量为e、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射，进入偏转电场区域，最后到达偏转器右端的探测板N，其中动能为Ek0的电子沿等势面C做匀速圆周运动到达N板的正中间．忽略电场的边缘效应．
